---

マクスウェル方程式に関して議論し、いくつかの種類の媒質中で、光波の伝搬、屈折、反射に関して議論していくことにする


マクスウェル方程式（Maxwell Equation）

光は電磁波の一種で一般的に次のマクスウェル方程式と呼ばれる４つの式でさまざまな現象を説明することができる。



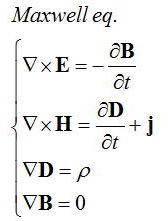
ベクトル量としてEは電場（V/m）、Hは磁場（A/ｍ）、Dは電束密度（C/ｍ２）、Bは磁束密度（T＝Wb/ｍ２）、ｊは電流密度（A/m２）

スカラー量としてρを（体積）電荷密度（C/ｍ３）、

物質中の性質をきめるパラメータとして誘電率ε（C/（V・ｍ））、透磁率μ（V・ｓ/（A・ｍ））、導電率（電気伝導度）σ（A/（V・ｍ））

と書くことにすると、



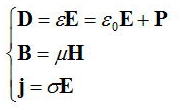
の関係があり、上記でε０（C/（V・ｍ））は真空の誘電率、Pは分極（C/ｍ２）

これらの式の意味の詳細を議論するのは、他の節で述べることにしてここでは割愛する。


２つの媒質の境界面における境界条件

マクスウェル方程式は、εやμなどの媒質の性質が連続的な領域（均一領域）で導かれた方程式である。

では、実際に、異なる２つの媒質の境界面（ｘｙ面）におけて、εやμが不連続的に変化しているとき

どのようなことが起こるのかを検討する必要がある。



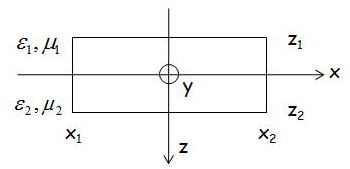
上図のように境界面（ｘｙ面）近傍の小さな矩形領域を考えて、Maxwell方程式の第一式のｙ成分に関して積分すると、



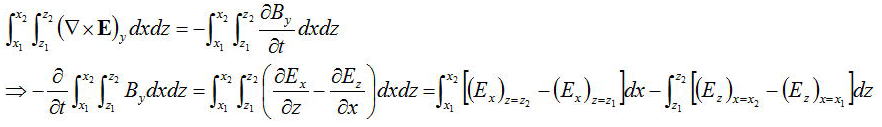
上式でｚ１、ｚ２を限りなくともに境界領域ｚ＝０まで近づけると、被積分関数は有限であるので、ｄｚ＝０と考えられるので、

ｚに関しての積分は０になる。よって、次式の関係式が得られる。



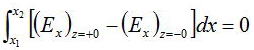
となる。積分範囲ｘ１〜ｘ２は任意に選べるので、



全く同様に、ｙｚ面でも成立するので、Ey成分に関しても上式が成立する。これが、境界条件とよばれ、

フレネルの法則等を導く際にこの境界条件を用いる。

ここでは、省略するが界面におけるD、B、Hについても上記のように計算すると界面前後での関係式を得ることができる。