
非吸収、均質等方媒質中の光波
非吸収・均質等方媒質中の光波に関して議論していく。非吸収・均質等方媒質中(誘電体・絶縁体)では、
j=σ=ρ=0でε、μはスカラー量である。このときマクスウェル方程式から、
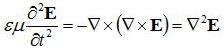
となり、磁場に関しても同様の式が成立する。
この方程式の解は、一般的には平面波、球面波、さらにガウスビームなどいくつかの形式があるが、
ここでは単純に単色正弦平面波として扱う。

となる。ここでkと媒質の定数ε、μには以下のような関係がある。
と表現すると、上記の2解偏微分方程式に代入し、時間項の偏微分を実行することにより
の空間のみの偏微分方程式(ヘルムホルツ方程式:一般解は煩雑なのでここでは議論しない)になる。
これに平面波の解を代入すると、
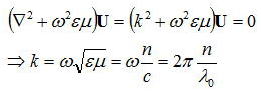
となり、媒質定数ε、μとkの関係が得られる。この式の意味は、
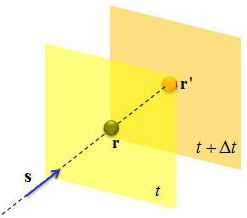
図のように時間t⇒t+⊿tに変化した後の平面波のようすを考えると、
平面波の解の位相量が同じときに同じ波面を見ていることになるので、どの程度波面が移動したのかを議論できる。
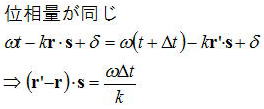
となり、r’-rとsとの内積が波面が進んだ量になるので、単位時間当たり、つまり⊿t=1あたりにω/kだけ移動したことになる。
ということは、この平面波の速度vは、
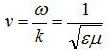
となり、この位相速度で波面が媒質中を伝搬していくことになる。また、誘電率と透磁率を真空の値にすると
光速cと等しくなり、およそ30万キロメートル毎秒の結果が得られる。
