---

この節では光が空間伝搬する際に、いくつかの例を交えて、どのように伝搬していくのかに関して議論していく

以前議論したようにマクスウェル方程式を整理すると、ダランベールの波動方程式が得られ



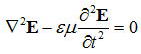
電場を時間項と分離して書くと



となり、上式に代入するとヘルムホルツ方程式が得られる。



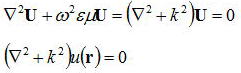
よって、上記から時間項を分離して、空間成分も３から１の成分において議論すればどのような光が伝搬するのかを議論できる。


エルミート−ガウスモード

ｚ軸方向に伝搬するスカラー場を



で表すと、関数ｆはｚに関して緩やかに変化すると仮定すると、ヘルムホルツ方程式は、



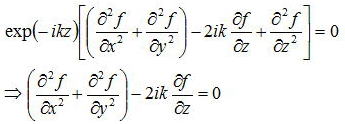
とｆの方程式となり、ｚから離れると詩集関数的に減衰する近軸解として、以下の式を考える。



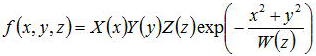
この式を代入して、変数分離をすると４つの方程式、



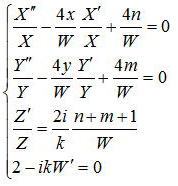
に分けられる。第一式と第二式はエルミート微分方程式であるので、



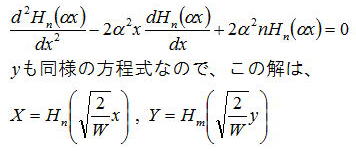
とエルミート多項式Hnを用いた解となる。また、第四式の解は、



となる。以上より、エルミート−ガウスモードの振幅は



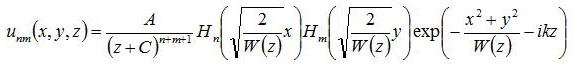
となり、後述（次節でのべる）するビーム半径、曲率半径、位相の遅れの項を取り入れると



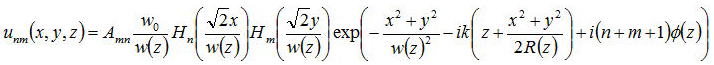
で与えられる。

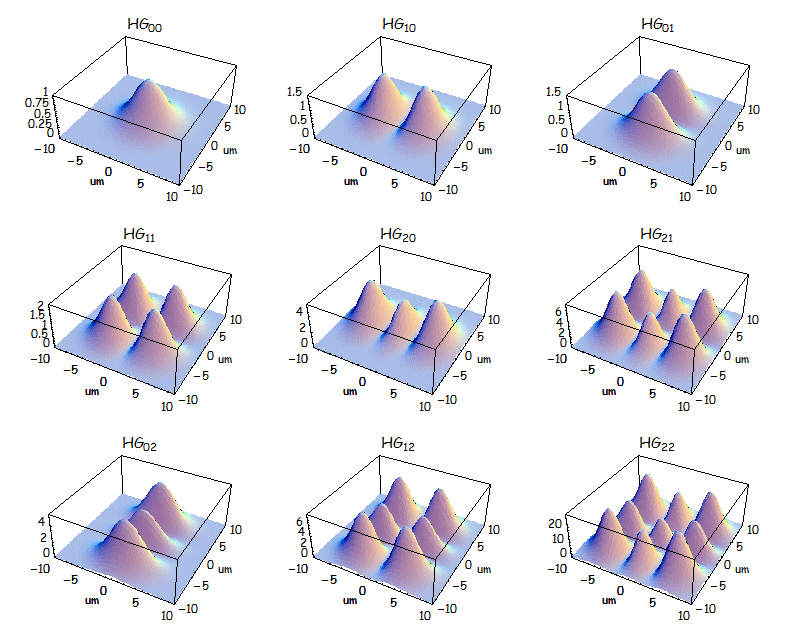
上式の強度分布は以下のようになる。