僈僂僔傾儞價乕儉
慜愡偱僄儖儈乕僩僈僂僗儌乕僪偱嬻娫揱斃偡傞岝偺嬻娫暘晍偵娭偟偰愢柧偟偰偒偨丅
僄儖儈乕僩懡崁幃偺揧偊帤乮値丄倣乯偱暘椶偝傟傞岝揱斃儌乕僪偺偆偪丄値亖倣亖侽偺嬻娫揱斃儌乕僪傪僈僂僔傾儞價乕儉偲屇傇丅
偙偙偱偼丄偦偺僈僂僔傾儞價乕儉偵娭偟偰媍榑傪恑傔偰偄偔丅 x^2+y^2=r^2偲偍偔偲
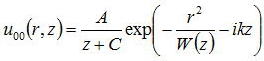
偲側傞丅偙傟傪僈僂僔傾儞價乕儉偲偄偆丅倸亖倸侽偱僈僂僔傾儞價乕儉偺攇柺偑暯柺偵側傞傕偺偲偡傞偲丄W=2乮倸亄C乯/乮ik乯
側偺偱丄
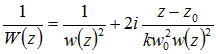
偲偐偗偰丄
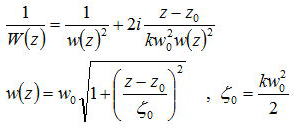
偲側傞丅兡侽偼儗僀儕乕儗儞僕偲屇偽傟偰偄傞丅倸亖倸侽偺柺傪價乕儉僂僃僗僩丄倵侽傪僂僃僗僩敿宎丄捈宎俀倵侽傪僗億僢僩僒僀僘偲偄偆丅
價乕儉峀偑傝妏
偙偙偱丄倸>>兡侽偺偲偒丄
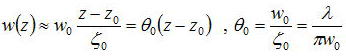
價乕儉僂僃僗僩偐傜墦偔棧傟偨埵抲偱偺僈僂僔傾儞價乕儉偺峀偑傝妏偱偁傞丅
價乕儉偺峀偑傝偺巜岦惈傪峫偊傞偲丄抁攇挿傎偳丄偝傜偵丄價乕儉僂僃僗僩偑戝偒偄傎偳丄峀偑傝妏偑彫偝偔巜岦惈偑彫偝偄丅
徟揰怺搙
偝傜偵丄價乕儉僂僃僗僩偑嵟彫敿宎倵侽偺併俀攞偵側傞斖埻傪徟揰怺搙乮Depth of Focus丟DOF乯偲偄偆丅
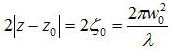
偲偁傜傢偝傟傞丅偮傑傝丄挿攇挿偱僂僃僗僩偺彫偝偄價乕儉傎偳徟揰柺偑柧妋偵側傞丅偙偺傆傞傑偄偼價乕儉偺巜岦惈偲偼媡偱偁傞丅
攇柺嬋棪敿宎
偝傜偵丄埵憡崁乮巜悢娭悢偺堷悢偺嫊晹乯偵拝栚偡傞偲丄
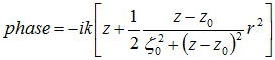
偲側傞偑丄暯柺偐傜偺偢傟傪昞偡埵憡検傪嚈倸偲偡傞偲丄忋婰偺戞堦崁偑ikz偑暯柺攇側偺偱丄
壓偺恾偵帵偡傛偆偵暯柺偲媴柺攇偐傜偺偢傟検嚈倸亖倰丱俀/俀R側偺偱丄埵憡崁偲斾妑偡傞偙偲偵傛偭偰埲壓偺幃
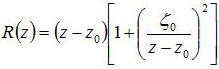 丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂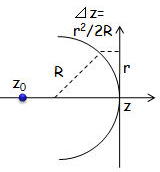
偺傛偆偵嬋棪傪昞偡偙偲偑偱偒傞丅
幃偺曄宍乮Guoy埵憡丗僌僀埵憡乯
僈僂僔傾儞價乕儉偺昞幃傪嬋棪敿宎R乮倸乯偲價乕儉僂僃僗僩倵乮倸乯傪梡偄偰彂偒側偍偡偲丄
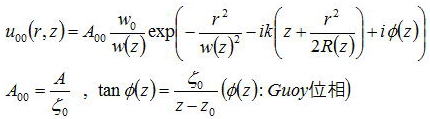
偲偐偗傞丅偙偙偱尵偆冇乮倸乯偼埵憡偺抶傟偲偟偰Guoy埵憡乮僌僀埵憡乯偲屇偽傟傞丅
岝僷儚乕
僈僂僔傾儞價乕儉偵傛偭偰塣偽傟傞岝僷儚乕偼
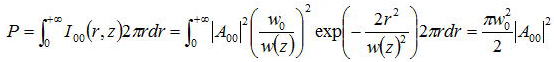
偲側傝丄敿宎倎偺椞堟偵娷傑傟傞僷儚乕偺斾棪偼丄
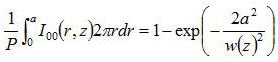
偲側傞丅壓偺寁嶼寢壥偑丄攇挿0.8um偱嵟彫價乕儉敿宎5um偺偲偒偺墶幉價乕儉抐柺敿宎倎側偄偵娷傑傟傞僷儚乕斾棪偱偁傞丅