---

マクスウェル方程式に関して議論し、いくつかの種類の媒質中で、光波の伝搬、屈折、反射に関して議論していくことにする

まずは非吸収・均質等方媒質中の光波に関しての説明を行う

非吸収・均質等方媒質中の光波

スネルの法則（Snell's law）



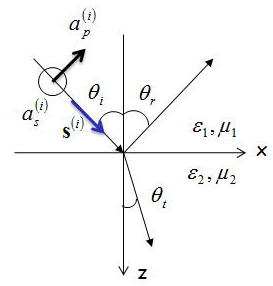
平面波として電磁場の伝搬を考えた際に、一般的に以下のように表現できる。



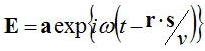
上記のように境界面ｘｙにおいては、位置ベクトルｒのｚ成分は０であるので、入射光は、



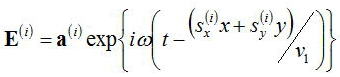
となる。反射光は（ｉ）⇒（ｒ）に変更すればよい、透過光に関しては、



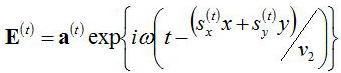
であらわされる。ここで、ここで、ｖ１、ｖ２は媒質１と媒質２中を伝搬する光波の位相速度である。

境界面において、三つの並みの位相は連続であるので、以下の式が成立する。



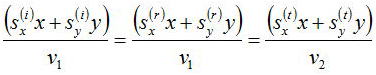
しかも、この式は境界面上のｘ、ｙ任意の点で成立するため、ｘ、ｙの係数がそれぞれ独立に等しいとして、

　　　

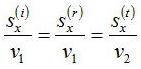
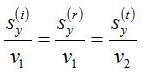
入射面をｘｚ平面にとるとｓｙ(i)＝０であるので、反射光と透過光のｓのｙ成分すべてが０となる。

よって、ｓｘ成分を角度θを用いて整理しなおすと、



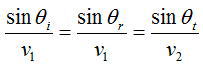
上式から、



入射光と反射光が境界面に対して等しい角度となることを示す。このことを反射の法則と呼ぶ

さらに、入射光と透過光に関しては



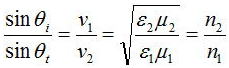
の関係が成立する。上式を屈折の法則、もしくはスネルの法則という。