
非吸収、均質等方媒質中の光波
非吸収、均質等方媒質中の光波の伝搬、屈折、反射の幾何学的な関係を述べてきた。
次に、その反射率と透過率がどのような数学的な記述が可能であるか議論していくことにする
フレネルの法則(Frenel's law)
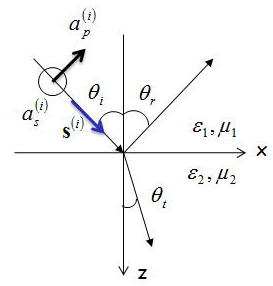
先ほどの節で議論した入射波、透過波、反射波の電場ベクトルEを入射面に平行と垂直な成分に分ける。
ドイツ語で平行と垂直を意味するpararellとsenkrechtを添え字として使うと、
ます電場ベクトルEの入射面に平行な成分p成分(p偏光)を考えると、
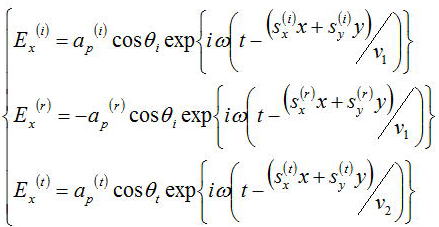
となる。磁場ベクトルに関しては、ここでは証明しないが以下の関係がある。
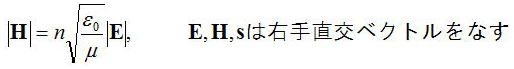
この関係を用いると、
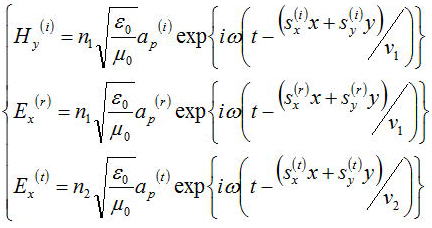
境界条件からE,Hの境界面に平行な成分は連続であるので、
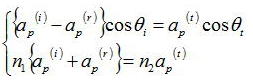
これらの式から、
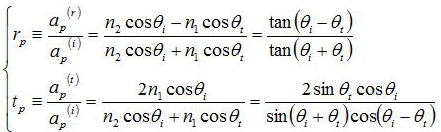
電場ベクトルEの入射面に垂直な成分、つまりs成分(s偏光)に関しても同様に考えて扱うと、
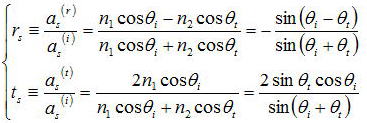
上式のp偏光とs偏光の反射率と透過率の関係式は、フレネルの法則として知られている。
p偏光に関しては特に面白い特徴がある。反射率の式において、
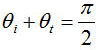
を満たすとき分母が発散するため、rp=0、つまりp偏光が全く反射しないことを意味する。
この特徴的な入射角度をブリュースター角(偏光角)といい、
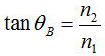
となる。
この関係式を用いてガラス(屈折率1.5)に光が入射するときの反射率と透過率の入射角依存性を検証してみる
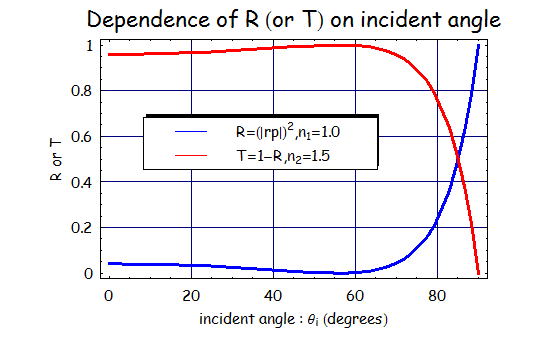
フレネルの法則からP偏光の反射率と透過率の角度依存性を求めた結果が上図である。
①入射角度56度近傍で反射率が0になっている
②入射角度0度では反射率が4%である
この2点は記憶するに値する結果である。
さらにs偏光に関して検討を進めると、
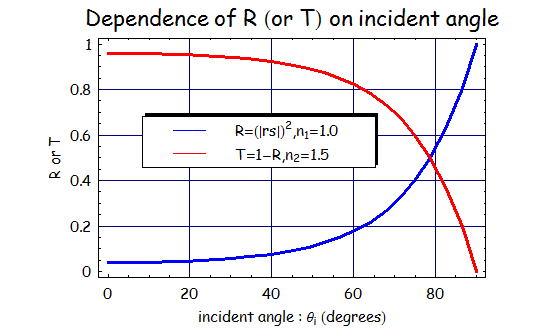
s偏光に関しては
①p偏光と異なり反射率が0になる角度は存在しない
②入射角度0度のときの反射率はp偏光と同様に4%である
上記の結果から考察するに、太陽からくる光は基本的には無偏光と考えられる。
空気中の散乱や障害物等の散乱により、S偏光とP偏光はいくつも散乱されて空気中を伝搬している。
ところが、散乱、反射というのは上記に示したようにS偏光とP偏光に偏りを生じさせる。
このため、ある方向の光を見た際に偏光の偏りが生じることがある。
(実は、太陽の出ている方向に対して90度の方向の光を見た際にその効果が一番大きくなる)