
吸収、均質等方媒質中の光波
次に吸収、均質等方媒質中の光波の説明を行う。
このような媒質は金属や半導体のような導電性をもち、従って吸収性のある場合に関しての取り扱いである。
ただし、異方性がなく均質等方な媒質の場合に関しての場合である。
まず、最初の議論は、マクスウェルの方程式に関してであるが、導電性があるが帯電していない場合、このような場合
電荷密度ρは0と考えたマクスウェル方程式を立てればよい。というのは、誘起された電荷は短時間の間に0となるため、
このように考えても差し支えがないからである。
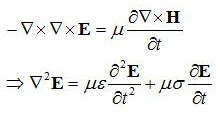
上式をもとにこの方程式の解を求めると、

の平面波が複素屈折率の媒質中を減衰しながら伝搬する解が得られる。
ここでの解は、複素波数、複素位相速度、吸収係数(減衰指数)、吸光係数(消衰指数)、複素誘電率等を用いて
いくつかの表現の仕方があるがどの表現の仕方を用いてもいいが一般的に複素屈折率か複素誘電率を用いるものが多いと思われる。
ところで、非吸収媒質から吸収媒質へ光が入射する場合、境界面での反射屈折に関しては、
境界条件、屈折の法則、フレネルの反射・透過係数の表式は屈折率として複素屈折率を用いれば、全く同じ形で表現できる
というありがたい結果となっている。
次の節で各法則の詳細を議論していこうと思う。
