---

吸収、均質等方媒質中の光波

屈折の法則


前節では、非吸収媒質から吸収媒質へ光が入射する場合、境界面での反射屈折に関しては、

境界条件、屈折の法則、フレネルの反射・透過係数の表式は屈折率として複素屈折率を用いれば、全く同じ形で表現できる

という点を見てきた。ここでは、屈折の法則に関して議論していこうと思う。



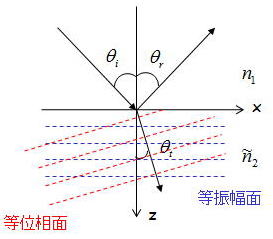
図に示すように境界面ｘｙにおいて平面波が非吸収媒質（屈折率ｎ１）から吸収媒質（屈折率ｎ２）へ入射した場合を考える。

このような媒質間の間でも屈折の法則は成立するので、



となる。このときｎ２は複素数となるのでθtも複素数となり、もはや単なる屈折角の意味を持たなくなる。

ここで、入射波の波面法線ｓ(i)がｘｚ平面に含まれているときには（そのような座標系をとることにして）、

透過波の波面法線ｓ（ｔ）のｘ、ｙ、ｚ成分を考察すると、



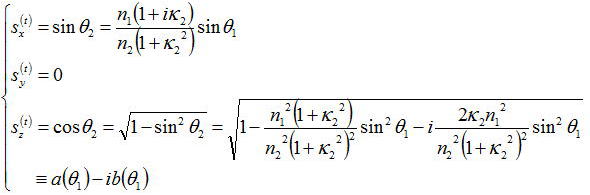
となる

この式を電場の式に代入すると、



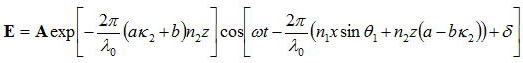
となる。これから、ｚ一定の面が等振幅面になることが分かる。

また等位相面は、Cosの位相項が一定である条件から、



で、この面に垂直な方向、つまり波面に対して垂直方向とｚ軸とのなす角度をθｔとすれば、



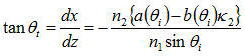
となる。これが意味するところは、スネルの法則は成立するが、波面に対して垂直な方向を直接求める際には、

上式を用いて計算しなければならないということである。

以上をまとめたイメージ図を上図にまとめてあるので参考にしてほしい。

結論としては、入射角θｉが０でなければ、等位相面と等振幅面が一致しないという事実である。