
吸収、均質等方媒質中の光波
フレネルの法則
前節では、非吸収媒質から吸収媒質へ光が入射する場合、境界面での反射屈折に関しては、
境界条件、屈折の法則、フレネルの反射・透過係数の表式は屈折率として複素屈折率を用いれば、全く同じ形で表現できる
という点を見てきた。次はは、フレネルの法則に関して議論していこうと思う。
一般的にθtは複素数であるので、
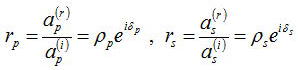
で表されるように、フレネル係数も複素数になる。この結果、電場の振動面が入射面とα(i)をなす直線偏光を入射すると、
α(i)=0,90°以外では反射光はふつう楕円偏光になる。
反射光の電場の振動面が入射面となす角(方位角、これも一般的に複素数となる)をα(r)とすると、
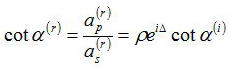
ここで、
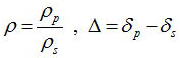
である。特に、⊿=Π/2に対応する入射角θiを主入射角いい、このとき反射楕円偏光の主軸は入射面に平行および
垂直になる。さらに上式でρei⊿cotα(i)=1ならば円偏光になる。これらの関係は、偏光解析法といって、偏光を用いて吸収性試料
の屈折率や薄膜の厚さと屈折率などの測定をする場合によく用いられる。
p偏光またはs偏光を入射した場合の反射率Rp、Rsは複素数n2を用いて計算しなおすと、
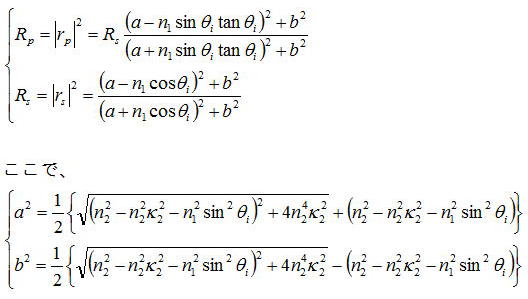
n1は第一媒質の屈折率、n2(1-iκ2)は第二媒質の複素屈折率である。
フレネル反射係数を、波長589.3nmにおける銀、アルミ、金の複素屈折率はn2-in2κ2の値は
0.20-i3.44、 1.44-i5.23、 0.47-i2.83
である。これらの数字を用いて、どの程度反射率があるのか、また、非吸収媒質では議論しなかったが位相変化⊿を検討し
楕円偏光になることを示すことにしよう。
まずはp、s波の反射率に関しては、
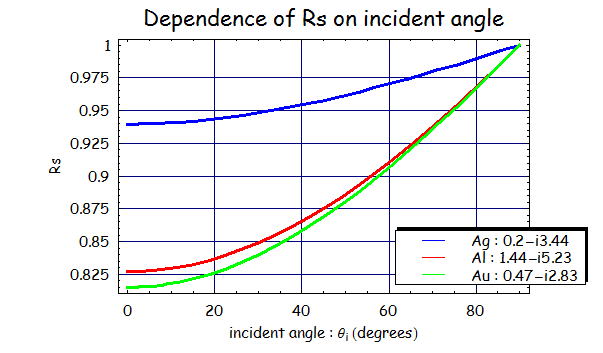
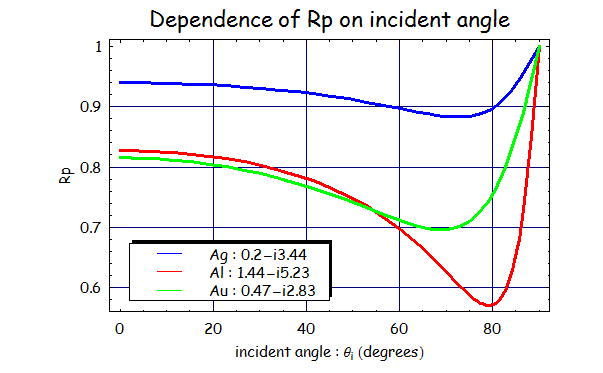
となる。まずs偏光に関しては、反射率が0度においても0に近くなくある程度大きな値で0.8程度の割合で反射する
という点にある。非吸収媒質では反射率がガラス空気間で垂直反射で4%しかないことを考えると大きな違いである。
p偏光に関しては、非吸収媒質では反射率が0となるブリュースター角が存在していたが、吸収媒質ではそのような角度はないが、
最小となる入射角度は存在する。このような角度を準偏光角(quasi-polarizing-angle)または偽偏光角(pseudo-polarizing angle)
という。この角度は主入射角(⊿=Π/2)と同じになる。
次に、p偏光とs偏光の反射後の位相変化を見てみると、
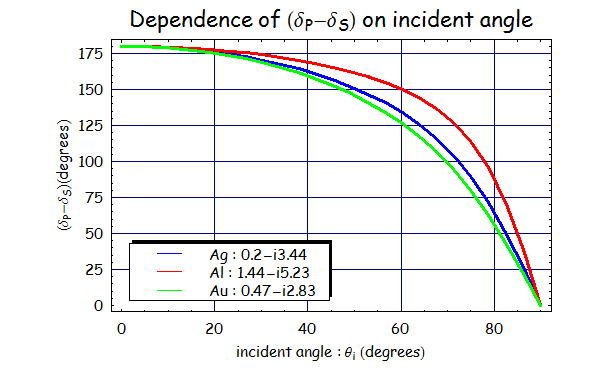
のようになっている。これは、非吸収媒質では反射の際、入射角度がブリュースター角の前後で反射により位相差が
Π変化していたのが位相変化なしで反射するという非連続的な位相差変化が起こるという事実があるが、
吸収媒質の場合、上記の結果から連続的に位相差がずれていくという結果が得られる。
つまり、この事実はp偏光とs偏光が位相差がΠ/2の円偏光であった場合垂直入射以外では
位相差が変化するため楕円偏光に変わることを意味している。
さらに位相差がΠ/2(円偏光入射で直線偏光出射)になる角度(主入射角)のとき、
Rpの反射率がほぼ最小になっていることを確認してほしい
