---

非吸収、異方性媒質中の光波

非吸収であるのでマクスウェル方程式中の電流密度ｊ=σ=0、また電荷ρも０と考える。

まず屈折率ｎの媒質中を伝搬する平面波について考えてみる。

誘電率εと屈折率ｎの関係は以下の式で表現できる。



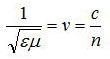
また光の波面の法線ベクトルｓをもちいて、



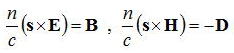
の関係がある。つまり、（波面法線と電場と磁束密度）の３つのベクトルは互いに直交しており、

さらに（波面法線と磁場と電束密度）の３つのベクトルも互いに直交している。

ここで、磁気的には等方性、すなわち透磁率μはスカラーで、電気的には異方性、すなわち誘電率εが

次式に示すような２階のテンソルで与えられる媒質、たとえば結晶に関して考察する。



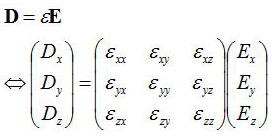
電束密度Dと電場Eは誘電率εの２階のテンソルを用いて上式で表現できる

電場と磁束密度は一般的にはテンソルで表現できることから、二つのベクトルは互いに平行ではないことがわかる。



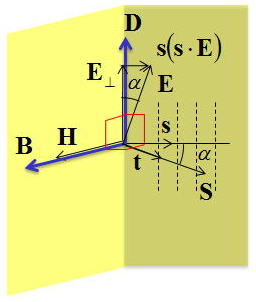
上記の図は各ベクトルの異方性媒質中での関係を表している。まず注目すべきなのは、エネルギーの伝搬を表すポインティング

ベクトルS=E×H（単位ベクトルｔ）の方向が波面法線方向ｓと角度αをなしており、波面の進む方向とエネルギーの伝搬する方向が

異なるということである。波面の進む速度を（位相速度：phase velocity）をvp=c/nとしたときエネルギーの伝搬速度、すなわち

光線速度（ray velocity）ｖｒは



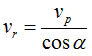
となる。

結晶はいくつかの対称性を持っており、その対称性から上記の誘電率テンソルは適当な直交座標系をとることによって、

テンソル成分を簡単にすることが可能である（群論＆線形代数）



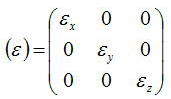
ここで、誘電率の各成分εx、εｙ、εｚを主誘電率という。ここで誘電率の関係によって次の三つに分類されている。



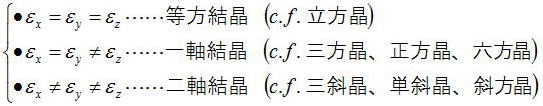
電磁波の持つエネルギー密度ｗを考えることで、屈折率との間に以下の屈折率楕円体と呼ばれる関係が得られる。



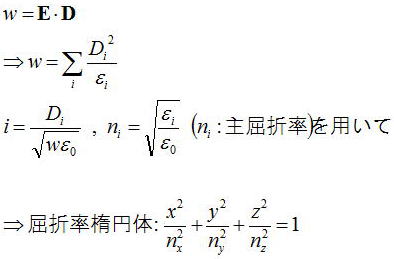
この屈折率楕円体に関する議論は次の節で詳しく述べようと思う。