---

非吸収、異方性媒質中の光波（屈折率楕円体）

この節では屈折率楕円体と光波の関係を議論していこうと思う

屈折率楕円体は電磁場のエネルギーの式から以下のように導かれた。



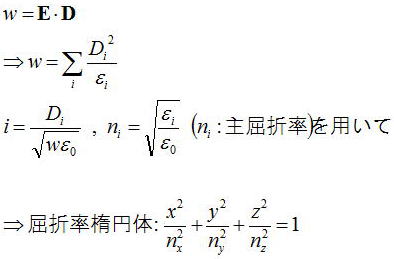
そもそもこの屈折率楕円体は、結晶の任意のｓの方向に伝搬する光波の電束密度Dの方向と

その方向に対応する屈折率の値を計算するときにとても有効な方法である。

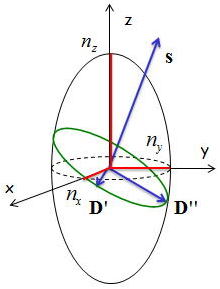
あるｓ方向を選んだとき、屈折率楕円体の原点を通りｓに垂直な面と楕円体の交線は楕円体なり、その二つの主半径の方向が、

Dの振動方向で、その大きさがそれぞれのDをもつ光波に対する媒質の屈折率となる。

それらの様子を表したのが下の屈折率楕円体の図である



ここで、もう少し数式的に上記の関係、ｓが与えられたとき結晶の屈折率がどのように与えられるのかを考察する。

透磁率μ＝μ０のとき、



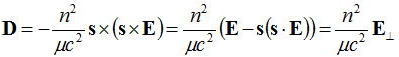
となるので、



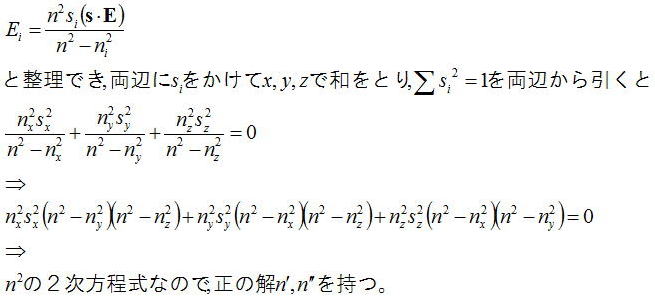
このことから、波面法線ｓを与えると、二つの屈折率が決まる。

次に、一軸結晶の場合、つまり、



とあらわすことにすると、先ほどの屈折率ｎの２次方程式は、



とあらわされる。ここでψを波面法線ベクトルｓがｚ軸となす角とすれば、上式の２つの屈折率は以下のように与えられる。



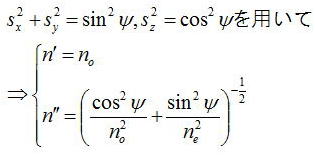
下の図はno<neおよびno>neの場合の２つの屈折率の様子を表した図である



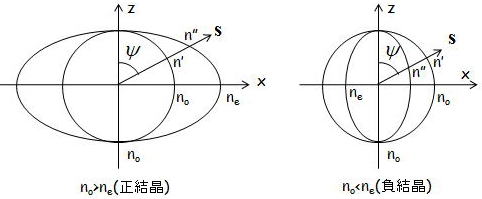
屈折率n'の軌跡は、球面で光の伝搬方向に依存しないので、この屈折率に対応する光波を常光線（ordinary wave）

と呼ぶ。また、n"は光の伝搬方向に依存するため、異常光線（extraordinary wave）と呼ぶ。

no>neを正結晶（c.f.水晶、氷など）、その逆を負結晶（c.f.方解石、ADP（Ammonium Dihydrogen-Phosphate）、LiNbO3など）とよぶ。

ｓがｚ軸と一致するn'＝n"ではこの方向二つの屈折率が一致する方向を光学軸という。

また、光学軸と波面法線を含む面を主断面といい、１軸結晶では、光学軸はただひとつで、２軸結晶では光学軸が二つ

あるため、これがそれぞれの名前の由来となっている。