Many-electron excitons and Fermi edge singularities in wide, parabolic(Al,Ga)As quantum wells
　phys. rev.B 　　M.Fritze 　　W.Chen　(1992)



1.Introduction
　
　2DEGにおいて変調doped-heterostructuresのcontact(電極)のない方法での研究が行われた。特に興味があるものとしては、2DのFermi seaとphotoexcitedしたholeとのCoulomb interactionであり、FESと呼ばれている多体系のenhancementをおこす。
理論的な観点からも実験的な観点からもそのmicroscopicな詳細の研究がInGaAs/GaAsの量子井戸でで行われた。
　本研究ではDoped Parabolic quantum wellsにおけるFESの興味深い現象を提供する。
まず、第一に3DのCoulomb interactionに関して取り扱う。第二に普通の変調dopedしてelectronとholeがspace-charge fieldでapartするような非対称の量子井戸に関してではなく強いelectronとholeの波動関数がoverlapするようなものを取り扱った。最後に磁場かにおけるedge-singularityと多体系のexcitonの問題を発展させる。


2.Sample
　　　　　　　　　　　　　　　　　　
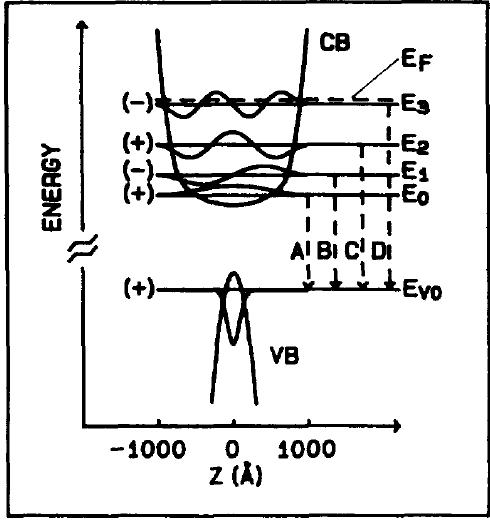
　今回用いたsampleはn-typeのmodulation-doped parabolic量子井戸である。この量子井戸を作るために、Al_xGa_1-xAsのAlの混成の割合を変化させた。井戸の真ん中ではx=0.19井戸の端(1000Å)ではx=0である。この井戸はGaAs/AlAsの超格子をサンドイッチ的にはさんだ。parabolic井戸の外側にspacer165Åをはさんでsheet状のsi-dopedした。
　netしたelectron densityは2.5×10¹¹cm^-2でありHall effectで測定した。
垂直磁場下でT=0.45KでFiber opticsでHe³cryostatで行った。photoexcited chargeによって系の変化がないのを確かめるために光学的にも伝導的(Hall effect)にも測定をした。
自己無頓着法によってparabolic potentialかつelectron-gasの静電場を考慮に入れて解かれたconduction bandのprofileはほとんどflatなものである。1000Åまでquasi-3Dのparabolic量子井戸と考えることができる。valence-band profileはz方向に半値幅が200ÅをもったGaussian envelop functionで近似できる。よって、band間遷移のquasi-3Dの光学遷移でsubbandはa few meVのenergy scaleである。
　バンド構造は上の図に示したとおりである。これによってelectronとholeは空間的に同じところに居続けようとしているのがわかる。
　　　　　　　　　　　　　　　　　　
　　　　　　
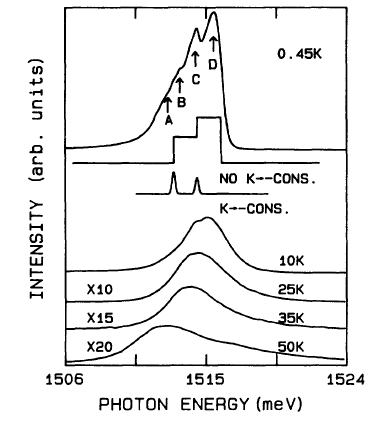
上の結果は温度依存性である（zero-magnetic field）。電子密度は2.5×10¹¹cm^-2、であり、自己無頓着による計算ではE₀=0.0meV、E₁=0.74meV、E₂=1.98meV、E₃=3.60meVである。ところで実験結果から解釈するとE₁-E₀=0.62meV、E₂-E₀=1.64meV、E₃-E₀=2.79meVであり、これらの不一致は驚くべきことではなく、それはelectronとholeのinteractionによるものであることがわかる。電子密度は2.5×10¹¹cm^-2に対応するFermi energyは3.81meV、これはE₃の端に対応する。
　もう一度、強調しておきたいのは今回扱った実験のサンプルはquasi-3D系の1000Å中に形成されたsubbandｓによるものである。
　PLに見られる4つのpeakに関して説明する。このpeakはFermi-edge付近で目立ったものになっている。これらのpeakは次の2つの温度依存性の性質を持っている。

　　(�@)　急激にpeakの識別ができなくなる。
　　(�A)　温度を上げるとhigh energyからlow enegy sideに移行してくる。(普通は高温になるとバンドギャップは小さくなる傾向があることが知られている。)
　
　ここで、筆者が言うことはphotoexcited holesとFermi seaのelectronsによる多体系の効果によるinteractionがlow-temperatureにおいてspectrumのenhancement効果を生み出すことを主張している。ここでphotoexcited holeの密度は10⁶cm^-2以下であることを付け加えておく。これらのenhancementはよくGaAs/InGaAsでも観測されている。しかも、これらの現象はMott(conventional exciton-electron-hole plasma)transitionという普通のtwo-body excitonic gasではelectron concentration and mesurement temperatureの観点から説明できない。
説明できない事柄は、
　　
　　(�@)　high enegy sideで発光強度が強くなっていること。
　　(�A)　量子井戸における選択則(しかしこれはparabolic quantum wellであるから一見普通の量子井戸のような選択則が成立してなくてもいいように思われるが、上でも強調したように今回扱っている系はquasi-3Dなのであるていどは従ってもいいように思われる。そのような意味で、今回のsampleで量子井戸での選択則が満たされていないことを強調しておきたい。)

　特に、満たさないと思われる選択則はBと特にD(ともに奇関数である)である。しかし発光は観測されている。このことは説明できなく、例えば対称性が敗れていることが原因であったとしても、二次イオン質量測定?(secondary ion mass spectroscopy mesurements)によってその影響は10%と以下である。
これらの観測は次に述べるSchottky gate experimentとmagneto-optical experimentでも証明される。
　大きな振幅のenhancement factorが理論的にも実験的にもFermi edgeでのＰＬで観測されることが期待され、観測された。それらは典型的なedge singularityではbinding energyは1meVのorderで鋭いexcitonlikeの構造をもっている。
これらはedge singularityを表していて、Fig.1で観測することができる。また、ＡＢＣのスペクトルに関してもそれに関連している。
　electron-hole interaction(頂点の訂正)とhole再正準化(自己エネルギーの訂正)は(あんまり意味不明だが)有限のconduntion-bandの混成がおこり、parityの選択則をこわす。これは、electronのFermi seaをとおしてedge singularityの侵入と明白なexcitonlikeのpeakの説明をするかもしれない。
完全な対称性を持った最低エネルギーのholeの状態は、多体のcoulomb　interactionもちろんconduction stateの混成はしえない。しかしながら有限の散乱とholeの跳ね返りによって価電子帯の対称性を弱めるだろう。散乱はrandomなAlの濃度の揺らぎのせいで弱い局在から見られると考えられる。
　ここでも主なポイントは"E₃のpeakの大きな確率がparityの禁止に大きく効いてくることを示す"という事実だ。




　複雑なmany-electron-one-holeの解釈として垂直磁場をかけてPL測定を行った。(T=0.45K)


　　　　　　　　　　　
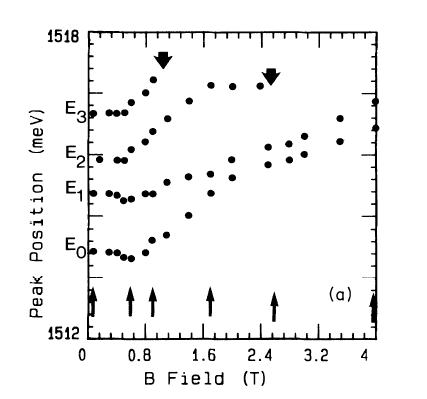
左の実験結果からは、4つのsubbandsからの発光が見られる。
１T以下では、ほんの少しのshiftがみられexcitonlikeであったが、これはfermi energy以下でのLandau-levelのspectrumをしめす、単一hetrojunctionや非対称量子井戸の結果とは対照的である。つまり、１Tでは、まだ強くholeとelectronがoverlapしていると考えられる。右図の計算結果からもquasi-３Dでは磁場の依存性は見られない。
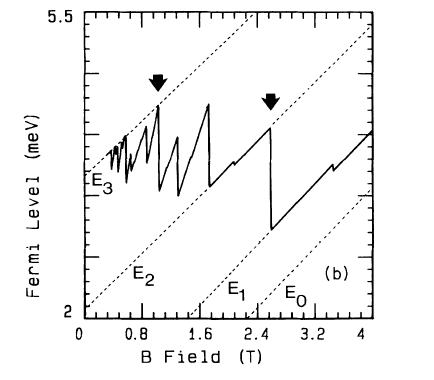
磁場の高いところでは、Landau-level-likeのような性質が見られた。それは、spectral shiftが増加し、fermi-levelがつぎのsubbandに落ちたときにhigher-subbandからの発光は消える。
fermi-levelの磁場依存性をsingle-particle-pictureの観点から計算した結果からも、消えるところは一致している。


　　　　　　　

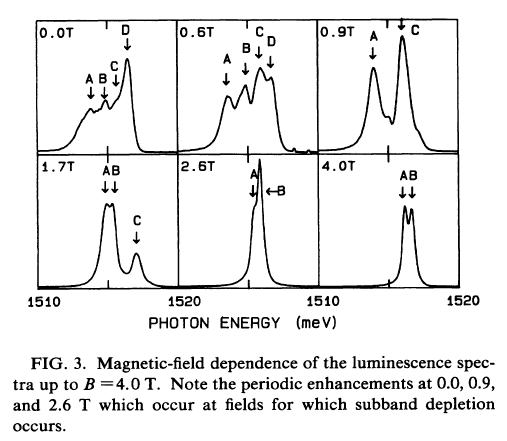
上の図は、fig.2で下からの矢印の磁場のときにFermi-edge-singularityによるenhancementが確認されたときのspectrumである。parity上禁止されているところで遷移が起こっているのが見て取れる。(B,D)。PLのこれらのenhancementはFermi-levelに電子がいるときかもしくはその近傍で起こっている。


　　　　　　　　　

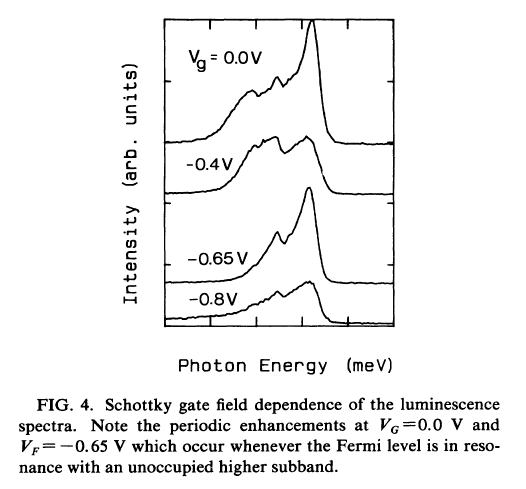
これらの周期的な構造は電子濃度を変えることでも(つまり直接的にFermi-levelをいじること)実現できることは容易に想像できるが、その結果が上に示したものである。