
Excitonic enhancement of the Fermi-edge singularity in a dense two-dimensional electron gas
丂phys. rev.B 丂丂M.Fritze 丂丂W.Chen丂(1992)
1.Introduction
丂
丂high-mobility 2DEG偼偄傠偄傠側interaction偺尋媶忋柺敀偄丄嵟嬤偱偼FQHE傗QHE偺optical signiture偺尋媶傕曬崘偝傟偰偄傞丅掕忢忬懺偺many-electron偲one-hole偺interaction傕棟榑揑偐偮幚尡揑偵嫽枴怺偔丄偙傟傜偺尋媶偼嵟弶偵Mahan偵傛偭偰bulk semiconductor偱峴傢傟偨丅斵偑帵偟偨偺偼暯峵忬懺偺electrons偵傛傞screening(coulomb interaction傪婲場偵偡傞)偵傛偭偰晛捠偼exciton偺岠壥偼尒傜傟側偄偼偢偱偁傞偑(娙扨偵尵偆偲偨傇傫exciton偺懇敍傪懪偪徚偡傛偆偵screening偑摥偔)丄揔摉側electrons density偱exciton-like effect偑尠嵼壔偡傞偙偲丄傑偨Fermi-edge偺偪傚偭偲壓偵bound忬懺偑偁傞偙偲傪(偙傟傜偼Mahan exciton偲屇偽傟偰偄傞)帵偟偨丅
偙偺bound忬懺偼
丂丂丂丂丂丂丂丂丂丂丂(侾)Fermi surface sharpness偲electron scattering
丂丂丂丂丂丂丂丂丂丂丂(俀)Pauli exclusion principle's restriction
偺寢壥偐傜棃傞傕偺偱偁傞丅(傜偟偄)
偺偪偵丄岝椼婲偱憹壛偟偨electron偺偆偪bound state偑偳偺掱搙unbound偵側傝丄continuum偵堏傞偺偐傪帵偡偨傔偵dynamics偺揰偐傜傕尋媶偝傟偨丅
媧廂偵娭偟偰偼FES偺崁偐傜尰傟傞怳摦巕嫮搙偺敪嶶偑Fermi-level偱偁傜傢傟丄偙偺傛偆側many electron excitonic feature偼2偮偺曗彏processes偱峔惉偝傟偰偄傞丅
丂丂丂丂丂丂丂丂丂(侾)hole偵傛傞electron scattering(vertex corrections)
丂丂丂丂丂丂丂丂丂(俀)the strong renormalization of the hole (self energy effects)
偵傛傞傕偺偱偁傞丅
丂偲偙傠偑偦傫側懡懱enhancement偼桳尷偺hole mass傗optical hole偵傛偭偰惗偠傞lifetime傗壏搙偺傛偆側broadening偵傛傞岠壥偵晀姶偱偁傞丅
FES偺岠壥傪尒傞偨傔偵偼丄2偮偺庤抜偑偁傞丅
丂丂丂丂丂丂丂丂丂丂(侾)broadening偺塭嬁傪嵟彫偵偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂(valence-hole偼慻惉偺梙傜偓偵傛傞偱bound偡傞丅偦偟偰hole偺桳岠幙検偼敪嶶丂丂丂丂丂丂丂丂丂丂丂丂丂偡傞丅偙傟傜偼InGaAs偺検巕堜屗偱娤應偝傟傞丅)
丂丂丂丂丂丂丂丂丂丂(俀)photo-hole偲Fermi level偱偺many-electron偲偺憡屳嶌梡傪戝偒偔偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂(偙傟偼杮榑暥偱徯夘偡傞丅娙扨偵尵偆偲丄Fermi-level偱偺photo-hole偲偺丂丂丂丂丂丂丂丂丂丂丂丂丂丂electron's scattering偼near resonant exciton偲偺憡屳嶌梡傪捠偟偰嫮傔傜傟傞丅)
丂丂丂丂丂丂丂丂丂
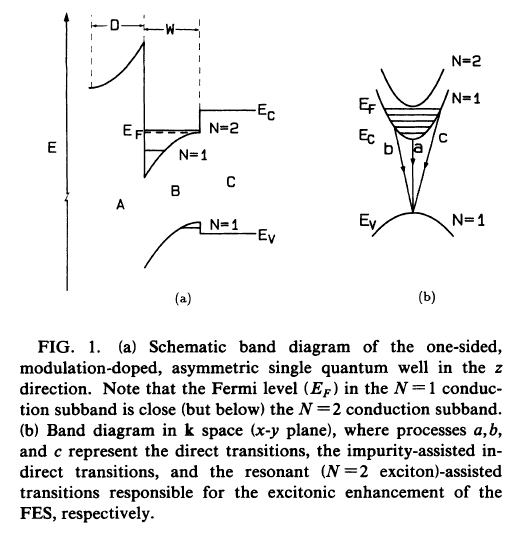
尋媶偵梡偄偨sample偼偍傕偵Fig1(a)偱偁傝丄one-side modulation doped asymmetric sigle quantum well偱偁傞丅
subband偺N=1偵娭偟偰偼丄A偲B偺奅柺偱偼揹巕偑60侌傎偳愼傒弌偟偰偄傞丅傑偨丄hole偼奅柺C偱偣偒偳傔傜傟偰偄傞偺偱hole偲electron偺wave function偼傎偲傫偳overlap偟偰偄傞偲峫偊傜傟傞丅
師偵N=2偺subband偵娭偟偰偱偁傞偑丄N=1傛傝a few meV崅偄丄検巕堜屗撪偺揹巕偺峀偑傝偼偍偍傛偦150侌偱偁傞丅N=1偲2偱偺堜屗撪偱偺overlap偺掱搙偼4偐傜8攞N=2偺傎偆偑戝偒偔側偭偰偄傞丅
拲堄偟偰傎偟偄偺偼崱夞偺幚尡偱偼N=2偵偼愯桳偟偰偄側偄偲偄偆偙偲偱偁傞丅偙傟偼N=2 exciton偲N=1偺FES偺嫟柭coupling偲偦偺2偮偺spectrum偺姳徛傪PL傪梡偄偰尋媶偡傞偵偼傕偭偰偙偄偺忦審偱偁傞偐傜偱偁傞丅
丂偙傟偐傜幚尡寢壥偺奣梫傪愢柧偡傞丅
捠忢偼N=2偼崱夞嬻偱偁傞偺偱丄N亖俀偺exciton偼俀D electron gas偲interaction偟側偄丅偲偄偆偺偼N=1偲僄僱儖僊乕偑嬤偄偨傔偵exciton偺暘嬌傪惗偠偝偣寢壥偲偟偰electron gas偲憡屳嶌梡偡傞偙傟偼揟宆揑偵偼0.6meV掱搙側偺偱柍帇偱偒傞丅崱夞偺応崌偺傛偆側偙偺interaction偲丄Fermi-level偲N=2exciton偺2偮偺慗堏偺嵎偺僄僱儖僊乕偑摨掱搙偺応崌偼暿偱偁傞丅偦偺偲偒FES偺怳摦巕嫮搙偼嫮傔傜傟偰N=2exciton偲嫟柭coupling傪捠偟偰擇寘傎偳嫮偔側傞丅
丂壏搙偵傛偭偰傕偮傛偄塭嬁偑尒傜傟傞T乣8K掱搙偱偙偺FESenhancement偼偒偊偰偟傑偆丅
丂摿偵in-plane偵帴応傪偐偗偰FES偺摿惈傪偟傜傋偨偑丄perpendicular偱偼揹巕偼Landau 検巕壔偝傟anticrossing傗oscillator strength sharing偑Fermi level偑N=2偵嬤偯偄偨偲偒偵尒傜傟傞丅PL偺廃婜揑側怳摦傕尒傜傟optical Shubnikov de Hass oscillations傕尒傜傟傞丅
師偵慗堏偵娭偟偰偱偁傞偑丄婎杮揑偵峫偊側偄偲側傜側偄傕偺偼丄師偺傒偭偮偺梫慺偱偁傞丅
丂(侾)攇悢k傪曐懚偝偣偰慗堏偡傞丅
丂(俀)晄弮暔宱桼偺娫愙慗堏丅
丂(俁)N亖俀偺exciton宱桼偺FES
(俁)偺僾儘僙僗偑堦斣嫽枴怺偄丅
2.InGaAs asymmetric single quantum well
A. general spectroscopic properties
丂傑偢丄GaAs偺僗儁僋僩儖傪尒傞慜偵InGaAs偺検巕堜屗偵娭偟偰偺幚尡寢壥傪傒傞丅幚尡憰抲偵娭偟偰偼13.5俿偺帴応偑偱傞傕偺偲two-俥倝倐倕倰(堦偮偼椼婲梡偱傕偆堦偮偼曔懆梡)傪梡偄偰峴偭偨丅sample偼嶰偮偺Al0.15Ga0.85As/In0.15Ga0.85As/GaAs偺扨堦偺旕懳徧検巕堜屗傪梡偄偨丅(S1,S2,S3)偙傟偼Fig.1(a)偲摨偠偱峔憿傪帩偭偰偄傞丅
帋椏偺摿惈傪昞偵昞偟偨丅偙偺應掕(Fermi energy and sheet density)偼Hall measurement偱應掕偝傟偨丅
丂丂丂丂丂丂
丂丂丂丂丂
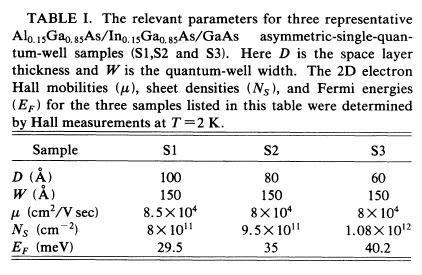
倂偼検巕堜屗偺暆丄俶s偼sheet density偲偟偨丅俶亖俀偐傜偺揹巕枾搙偼應掕偝傟側偐偭偨丅(偙傟偼Shubnikov-de Haas Oscillations傪Fourier transform傪尒傞偙偲偱偦傟偼傢偐傞丅検巕堜屗偺subband偺俶亖侾丄俀偺椉曽偺怳摦偺廳偹偁傢偣傪尒偰偄傞偐傜偱偁傞丅)
Fig.2(a)偼掅壏偱掅嫮搙偱應掕偟偨俹俴偱偁傞丅帴応偼B=0T偱偁傞丅
丂丂丂丂丂丂丂丂丂
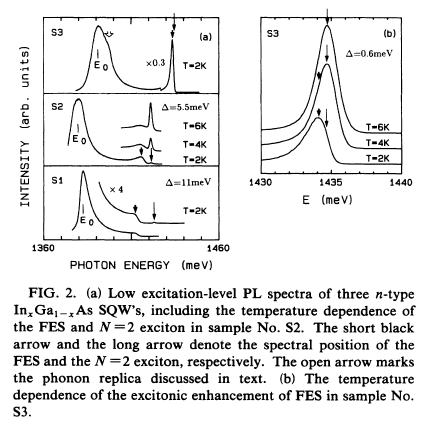
挿偄栴報偼俶亖俀偺exciton偱偁傝丄抁偄栴報偼FES偐傜偺敪岝傪尒偰偄傞丅儮偼擇偮偺敪岝偱偺僗儁僋僩儖偺僄僱儖僊乕嵎偱偁傞丅俤0偼k=0偱偺捈愙慗堏偱偁傞丅
丂S3偺sample偼儮偑彫偝偄丅偙偺恾偼Fig.2(a)偲(b)偱妋擣偱偒傞丅俶亖俀偺Storks shift攇娤應偝傟側偐偭偨丅偙傟偼僒儞僾儖偺幙偲俶亖俀偺exciton偺杮幙揑側惈幙傪斀塮偟偰偄傞丅
丂偙傟偐傜丄S1,S2,S3偵娭偟偰丄媍榑偟偰偄偔丅
傑偢丄S1偵娭偟偰偱偁傞偑丄
丂丂丂丂丂丂丂丂丂丂丂丂
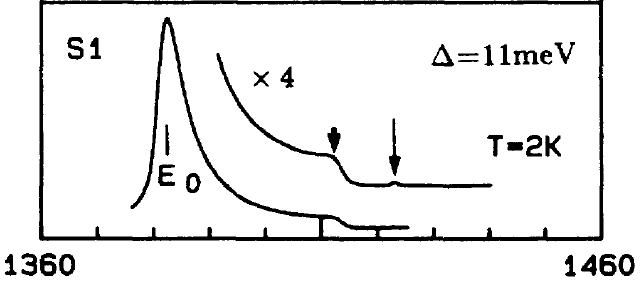
抁偄栴報偼N=2exciton偺塭嬁傪庴偗傞偙偲側偟偵N=1偺俀DEG偵傛偭偰桿摫偝傟偨FES偺柤巆偱偁傞丅N=2偲Fermi-edge偺僄僱儖僊乕偑棧傟偡偓偰偄傞偨傔偵(嚈=11meV)FES偺Exciton enhancement傪娤應偱偒側偄丅
堦斒揑偵InGaAs偺FES偼尦婥偑側偔峀偑偭偰偄傞丅偦傟偼丄僗僋儕乕僯儞僌偝傟偨electron-hole interaction偺岠壥傗桳尷偺暯柺撪偺light-hole mass偵傛偭偰偱偁傞丅(偼偀丠)
heavy-hole band偲light-hole band偼60meV暘楐偡傞丅(柺撪偱)偙偺偙偲偼Fig.2偱偼廳梫偱偁傞丅
S2偵娭偟偰偱偁傞偑丄
丂丂丂丂丂丂丂丂丂丂丂
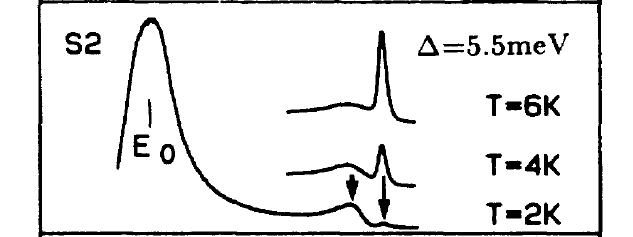
幚尡揑偵僄僱儖僊乕偺暘楐偼嚈=5.5meV偱偁傝丄T=2K偱偼偭偒傝偲exciton enhancement FES偑娤應偝傟偰偄傞丅壏搙偲偲傕偵徚偊偰偄偒8K偱偼尒偊側偔側偭偨丅偦傟偲偼懳徠偵exciton偺岠壥偑嫮偔側偭偰偒偰偄傞丅
S3偵娭偟偰偱偁傞偑丄
丂丂丂丂丂丂丂丂丂丂丂丂丂
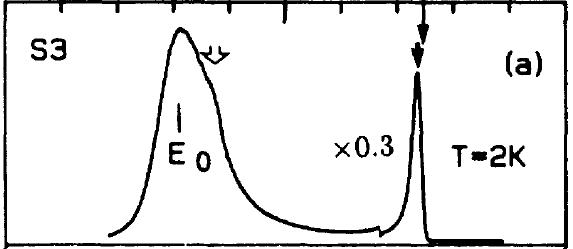
嚈=0.6meV偱偁傞丅偙偺幚尡偱偟傔偟偰偄傞偙偲偼丄FES偼N=2偺exciton偲嫟柭揑偵coupling偡傞偙偲偱PL偑嫮偔側偭偰偄傞偲偄偆偙偲偱偁傞丅偙偺壏搙埶懚偵娭偟偰偼壓偵帵偟偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
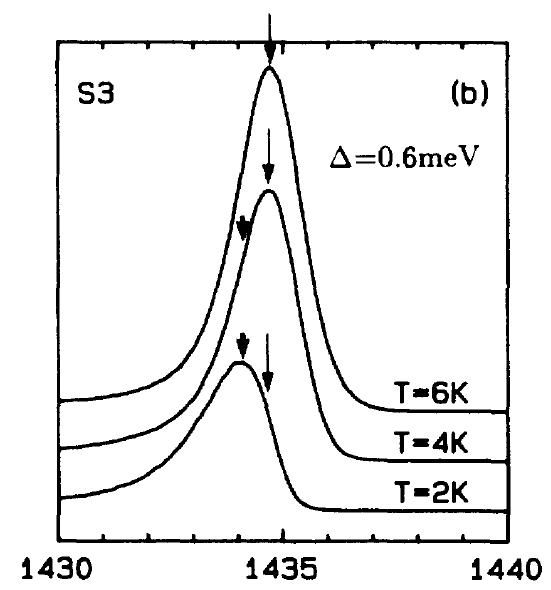
N=2偺exciton偑壏搙偲偲傕偵尠嵼壔偟偰偄傞偺偑尒偰庢傟傞丅2K偱偼旕懳徧偱偁傞偑丄6K偱偼懳徧偱偁傞丅偙偺嚈偺埶懚惈偵娭偟偰偼屻偵徻偟偔媍榑偡傞偙偲偵偟偰丄傑偢偙傟傜偺僗儁僋僩儖偵娷傑傟傞偄偔偮偐偺婎杮揑側僶儞僪娫慗堏偺崻杮傪峫嶡偡傞偙偲偵偡傞丅
嵞傃S1偵娭偟偰媍榑偡傞偑丄
E0偲FES偺敪岝偱energy separation偼30meV偱偁傞丅偙傟偼Hall effec倲偱偺應掕偲傛偔堦抳偟偰偄偰丄indirect transition偱偁傝丄pass(c)偱偁傞偙偲偑傢偐傞丅僄僱儖僊乕偺崅偄傎偆偱偁傞偑偙傟偼丄敪岝嫮搙偼傕偟捈愙慗堏側傜
丂師偵晄弮暔偵傛傞塭嬁偵娭偟偰峫嶡偟偰傒傞丅
俀Delectron偼僗儁乕僒乕憌偺僀僆儞壔donors傗慻惉偺梙傜偓偵傛傞ramdomly impurities 偵傛偭偰InGaAs偺PL偺僗儁僋僩儖偺宍偵塭嬁傪媦傏偡丅曄壔偟側偄k偲偄偆偺偼傕偼傗偙偺傛偆側嶶棎偺懱宯偱偼傛偄検巕悢偵偼側傝偊側偄丅傛偭偰丄k偑僛儘偱側偄electron偼k=0偺photohole偲嵞寢崌敪岝偟偆傞丅幚嵺偵偙偺崅師偺岠壥偼偼彫偝偄偑丄掅壏偱丄椼婲嫮搙偑彫偝偄偲偒偵偼photohole偼偡偖偵k=0偵娚榓偟偰丄Fermi-level偵direct transition偡傞偨傔偺hole偑偄側偔側偭偰偟傑偆丅偙偺棟桼偑direct transition傛傝indirect transition偺傎偆偑敪岝嫮搙偑嫮偔側傝偆傞棟桼偱偁傞丅
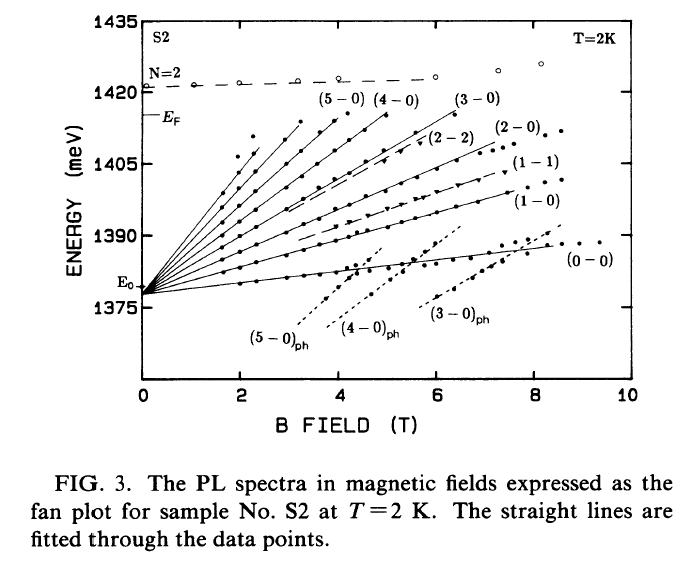
偙傟偼 E0偺N=1偺subband偺敪岝偲丄帴応偺僗儁僋僩儖偐傜媮傔偨N=1偺敪岝偲斾妑偡傞偲1.2meV掱搙 (Fig.3)bule shift偟偰偄傞偙偲偐傜偙傟偼impurities assisted 偵傛傞崅師偺敪岝偺塭嬁偑娷傑傟偰偄傞偙偲偑敾抐偝傟傞丅
摉慠丄偙偺岠壥偼spacer偺峀偝偵埶懚偡傞傢偗偱丄(偦傟偼spacer偺峀偝偵傛偭偰梙傜偓側偳偺僷儔儊乕僞乕偑堎側傞偐傜偱偁傞)敄偄spacer偺傎偆偑E0偺peak偼峀偑偭偰偄傞丅
丂Fig.2(a)偺S3偱偼LO phonon偺塭嬁偑尒傜傟傞(敀敳偒偺栴報)丅偙偺indirect transition偼InGaAs偱偼fermi emergy偑36meV埲忋偺傕偺偱娤應偝傟傞丅
師偵丄悅捈帴応傪擖傟偨偲偒偵娭偟偰峫嶡偡傞丅
帺桼揹巕偲hole偼Landau level偵検巕壔偝傟傞丅崱夞偼N=2(検巕堜屗)偺僒僽僶儞僪偵偼揹巕偼懚嵼偟側偄偙偲傪transport偺幚尡偱帵偟偨丅N=2偺exciton偺岠壥偼拞惈偺偨傔偵transport偵偼堷偭偐偐傜側偄丅偙傟偼岝妛偺幚尡偲揱摫偺幚尡偺戝偒側堘偄偱偁傞丅
丂丂丂丂丂丂
丂丂丂丂丂丂丂丂
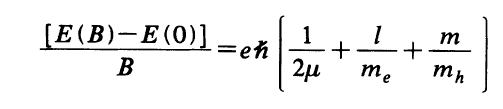 丂丂丂丂
丂丂丂丂Landau level偼挷榓怳摦巕偺傛偆偵側傞偺偱丄electron subband and hole subband偺椉曽傪峫椂偟偰寁嶼偟偨傕偺偑忋偺幃偱偁傞丅忋偺寢壥偼偲偰傕嫽枴怺偄丄偲偄偆偺偼晛捠diagonal(l=m)偺敪岝偑嫮偔尒傜傟傞偺偱偁傞偑丄掅壏偱偁傞偲off-diagonal偺impurity scattering偺傎偆偑嫮偔娤應偝傟傞丅偙傟偼photohole偑嵟掅偺landau level偵偟偐愯桳偟偰偄側偄偐傜偱偁傞丅幚嵺偺敪岝僗儁僋僩儖偼Fig.4偵帵偟偨丅偙偙偱丄傗偼傝師偺偙偲偺偒偯偔丄偦傟偼丄愭傎偳傕弎傋偨傛偆偵偙偺崅師偺岠壥偼晄弮暔偵傛傞傕偺偩偭偨傝丄慻惉偺梙傜偓偵傛傞傕偺偩偲偡傞偲spacer偺戝偒偝偵埶懚偡傞偼偢偱偁傞丅S1偲S2傪斾傋偨偲偒偵偙偺傆傜偮偒偺戝偒偄傎偆偼丄S2偺傎偆偱偁偭偨丅偲偄偆偙偲偼丄偙偺off-diagonal偺敪岝偼S2偺傎偆偑戝偒偔側傞偺偼憐憸偡傞偵擄偟偔側偄丅幚尡寢壥傕偦傟傪帵嵈偟偰偄傞丅
丂丂丂丂丂丂丂
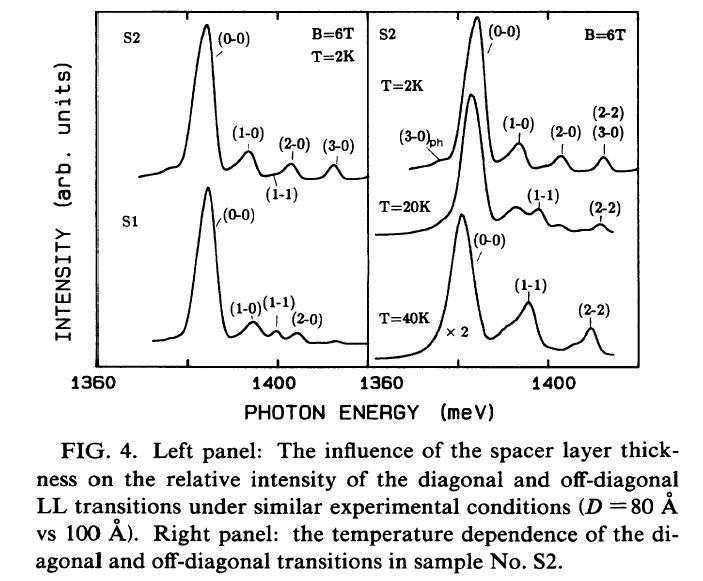
傑偨壏搙埶懚惈傕嫽枴怺偄丅偦傟偼丄愭傎偳傕弎傋偨傛偆偵off-diagonal偺敪岝偑掅壏偱偼嫮偔丄崅壏偱偼diagonal偺敪岝偑嫮偔側偭偰偄傞丅偮傑傝丄崅偄Landau level偺傎偆偱擬揑側population偑尒傜傟傞偐傜偱偁傞丅(l-m)偺偆偪丄(3-0)偲(2-2)偼弅戅偟偰偄偰嬫暿偱偒側偄偑丄偙偺壏搙埶懚惈偑堘偆偙偲傪棙梡偡傞偲嬫暿偱偒傞丅壏搙傪崅偔偡傞偲band-gap偑彫偝偔側傞偺偱僗儁僋僩儖偼慡懱揑偵redish偡傞偑Landau-level偼塭嬁偼弌側偄丅傛偭偰慡懱偑暯峴堏摦偟偨傛偆側傕偺偵側傞丅
InGaAs偺偲偒1-LO-photon傪曻弌偟偰敪岝偟偰偄傞僗儁僋僩儖偑尒傜傟傞丅偙傟偼1-photon energy偼36meV偱偁傞丅偙傟偼丄Fig.3傪傒傞偲暯峴偵1-photon暘壓偑偭偨偲偙傠偵尒傞偙偲偑偱偒傞丅(0-0)偲偺crossing偼anti-crossing偱偁傝斀敪偟偰偄傞偺偑尒偰傢偐傞丅帴応偱尵偆偲4.5T 5,5T 7,7T 偱偙偺anticrossing偑偍偙偭偰偄傞丅
B.Excitonic enhancement of FES by the subband resonance condition: tuning in parallel magnetic fields
丂丂丂丂丂丂
丂偮偓偵丄榖戣傪FES偺exciton enhancement偵娭偟偰徟揰傪峣偭偰峫嶡偟偰偄偔丅
崱夞偺Fig.2偺偙傟傜偺僗儁僋僩儖偼Fermi-surface偐傜偺敪岝偑N=2偺Exciton偺敪岝偲憡娭偑偁傞偲峫偊傜傟傞偙偲傪愭傎偳尒偨丅偙傟偼丄埲慜偐傜抦傜傟偰偄傞states mixing偑婲偙偭偰偄傞偲峫偊傜傟傞偑丄崱偺応崌偼偦傟偲偼堎側偭偰偄偰懡懱栤戣偑娷傑傟偰偄傞偺偱暋嶨偱偼偁傞丅
偙偙偱偼丄偙傟傜偺暔棟揑側夝庍傪parallel magnetic fields偺幚尡寢壥偲斾妑偡傞偙偲偱媍榑偡傞丅
崱夞偼擇偮偺梫慺傪峫偊側偄偲側傜側偄丅1偮偼diamagnetic shift偵傛傞exciton傊偺岠壥丅傕偆1偮偼擄偟偄偺偱偼偁傞偑丄electric and magnetic confinement偺桳尷偺崿惉偵傛傞2DEG偺桳岠幙検偺憹壛偑Fermi-energy傪彫偝偔偝偣傞岠壥丅
拲栚偟偨偄偺偼10T偱偼丄N=2 exciton Bohr radius 偼150侌傑偨丄帴婥挿(偁傞堄枴僒僀僋儘僩儘儞敿宎)偼80侌偱偁傝丄N=1偱偼倸曽岦偺暵偠偲傔偑60侌偱偁傞偙偲偵拲栚偟偰偍偒偨偄丅
diamagnetic shift偼4T傑偱偼栺1meV偱偁傝丄6乣10T傑偱偼4meV掱搙偱偁傞丅
偙傟傜偺2偮偺岠壥偵傛傞偢傟偼enhancement偺岠壥傪偪傚偭偲廋惓偡傞偩偗偱傛偄丅
丂丂丂丂丂丂丂
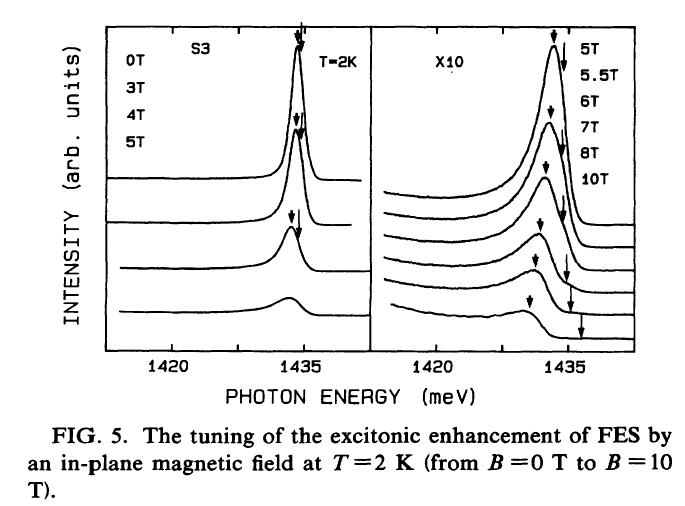
忋偺僌儔僼偼zero帴応偺PL偲斾傋傞偲5T偱偼6攞彫偝偔側偭偰偄傞丅偙傟偼excitont偺嫟柭偑2偮偺岠壥偵傛偭偰棧傟偰偄偭偰偄傞偐傜偱偁傞丅帴応傪戝偒偔偟偰偄偔偲傕偼傗exciton偺PL偼尒偊側偔側偭偰偒偰偄傞丅壏搙傪忋偘傞偲N=2偺愯桳偑戝偒偔側偭偰偔傞偺偱exciton偺岠壥偑傛傝慛柧偵尒偊偰偔傞偺偑Fig.6偱尒傞偙偲偑偱偒傞丅
傑偨丄B亜5T偱偼丄FES偺旕懳徧惈傪尒傞偙偲偑偱偒傞偑偙傟偼丄hole偺挼偹曉傝傗桳尷壏搙偺岠壥傗晄弮暔偵傛傞level偺僽儘乕僪僯儞僌偑峫偊傜傟傞丅
丂丂丂丂丂丂丂丂
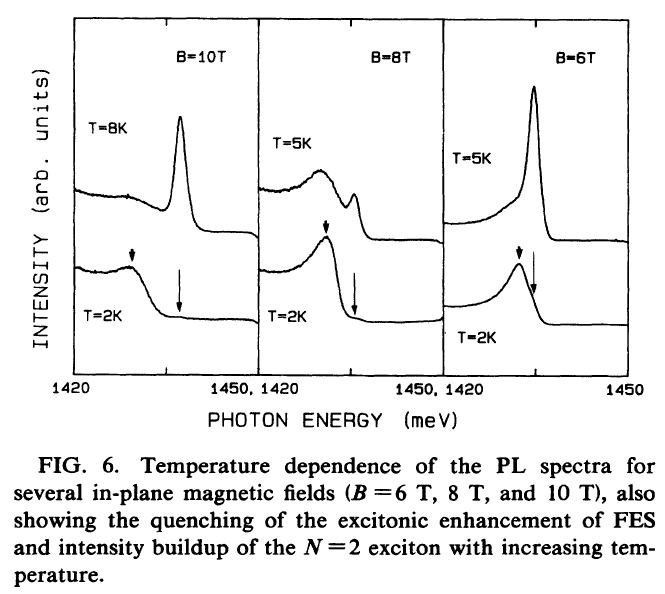
丂丂丂丂丂丂丂丂丂
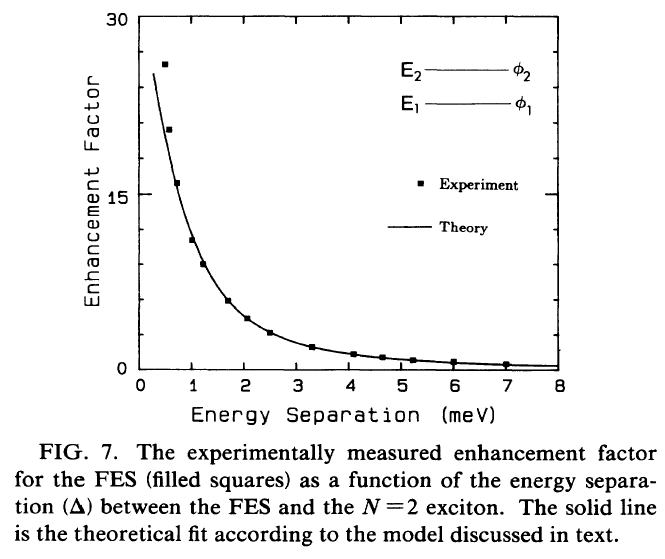
忋偺幚尡寢壥偼丄埲壓偺娙扨壔偟偨棟夝偵傛偭偰fitting偟偰偁傞丅
傑偢丄愛摦V偑擖傞慜偵偼2偮偺攇摦娭悢偼弅戅偟偰偄傞丅
1偮偼N=2偺exciton偺塭嬁偑偼偄偭偰偄側偄丄N=1偐傜側傞FES傪昞偡攇摦娭悢丄傕偆堦曽偼N=2偺exciton傪昞偡攇摦娭悢偱偁傝丄g偼ground state偺懡懱攇摦娭悢偱偁傞丅V偑崱峫椂偵擖傟偰偄側偄偺偱丄岝椼婲偝傟偨exciton偲俀DEG偼撈棫帠徾偱偁傞丅
1偺攇摦娭悢偱optical matrix element偼(N=2偺exciton偺岠壥偼擖偭偰偄側偄丅)
梫慺偲偟偰偼N屄偺2DEG偲岝椼婲偝傟偨electron偲hole偱偁傞丅岝椼婲偝傟偨傕偺偼嬻娫揑偵偼摨偠偲偙傠偵偁傞偺偱嵎偼僛儘偵偟偰偁傞丅
2偺攇摦娭悢偱optical matrix element偼
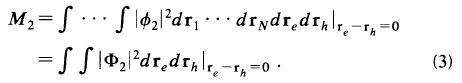
V傪偄偭偨傫擖傟傞偲丄interaction Matrix偼
偱偁傝丄N=2偺exciton state偼埲壓偺傛偆偵偐偗傞丅
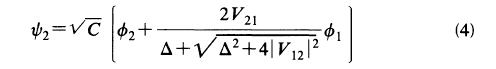
堦曽偱FES偺傎偆偼
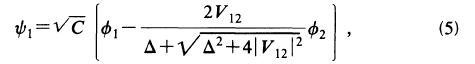
偱偁傞丅
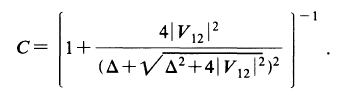
偼婯奿壔掕悢偱偁傞丅
寢崌偟偨屻偺optical matrix偼
FES偺enhancement偺岠壥偼
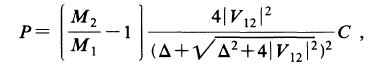
C.Effect of perpendicular magnetic fields: optival Shubnikov de-Hass oscillations
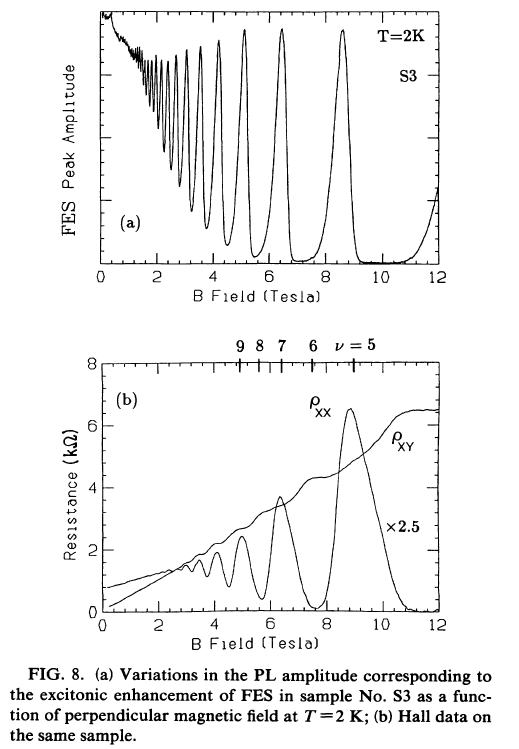
師偵丄悅捈帴応傪偐偗偨偲偒偵Landau level偵検巕壔偝傟偨傕偺傪傒傞丅Fermi level偱偺忬懺枾搙偼帴応偺媡悢偵斾椺偟偨戝彫偑孞傝曉偡廃婜揑側峔憿傪帩偮丅崱夞偼偦偺FES偱偺廃婜揑側怳摦傪尒傞偙偲偵偡傞丅
Fig.8(b)偲Fig.8(a)傪斾傋傞偲丄OS倓H偺傎偆偑侾T傑偱偼廫暘偵怳摦偑尒偊偰偄傞偑帴婥掞峈偱偺應掕偼偁傑傝偼偭偒傝偲嬫暿偡傞偙偲偑偱偒側偄丅偙傟偐傜丄OSdH偼Fermi-level偱偺忬懺枾搙偺巜昗偩偗偱側偔丄Fermi-level偑偳偙偵偁傞偺偐傪偼偭偒傝偲偟傔偡丅偲偙傠偑丄桝憲尰徾偱偼Fermi-level偱偺忬懺枾搙偩偗偑巜昗偵側傞丅偙傟偼FES偺exciton enhancement偑娭學偟偰偄傞丅
丂丂丂丂
丂
