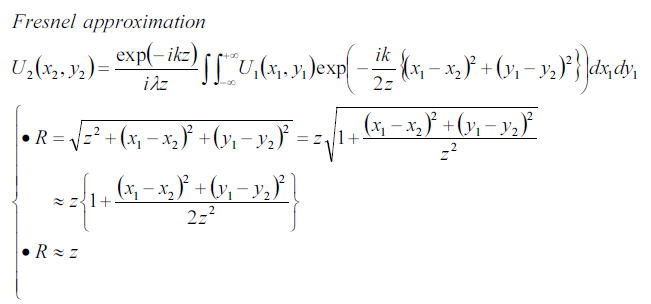まずキルヒホッフ回折理論(Kirchhoff diffraction)について説明する。
キルヒホッフの回折理論はホイヘンスの原理を数学的に表現したものである。
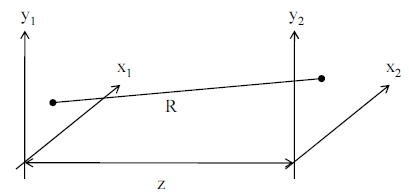
下の図に示しているようにx1、y1平面上のある点から出た光は振幅の大きさは1/Rで減衰し
(エネルギーはその二乗で減衰)伝達する。
そのためx2、y2平面の点(x2、y2)での振幅はx1、y1平面のすべての素元波の重ね合わせと考えられるため、
回折角が小さい領域(近軸近似)では
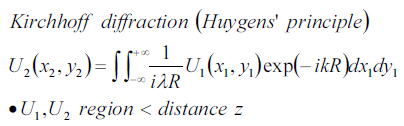
と記述できる。
Kirchhoffの回折理論はこのままだと計算することが難しい。そのため、まず、次の仮定をしさらに近似を行う。
その近似を行った式がフレネル(Fresnel)回折(近似)と呼ぶ。
近似領域では、Rとzとほとんど等しいが、指数はそのままzに近似できない。
それは、kがかかっているためでRとzの差が小さくてもその誤差量にkという可視光なら10の7乗程度
掛けられるので無視できなくなる。よって近似を以下のように行う。