---

先ほどまでいくつかの近似を行いフレネル回折まで説明してきた。
これでもまだ計算するには面倒であるので、以下の近似を行い、フラウンフォーファー回折に関して説明する。






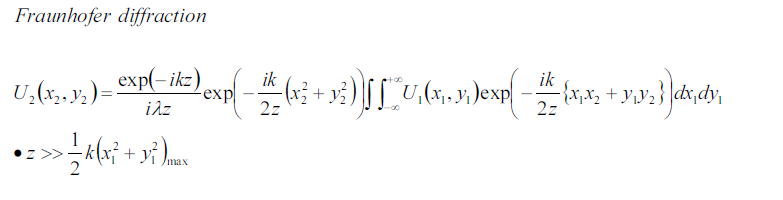
この近似を考察すると、ｋ≒1／λなのでｘ１＾２/(z×λ）＜＜１なのでｘ１が波長程度の広がりなら確実に成立する
さらに、ｚも十分に大きいため制約条件は波長を例えば600nmとし、右辺の１を0.1として、ｚとｘ１の関係を考えると



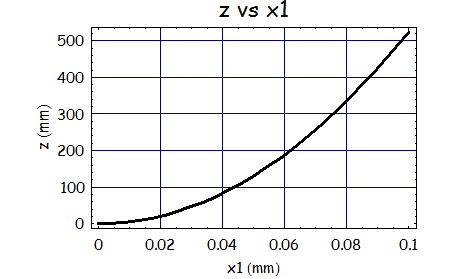
となる。ソースU1の広がりとして0.1ｍｍ、回折した光を投影するスクリーンの先は500ｍｍ程度の範囲で成り立つ式である。
しかも上式をよく見てみると、回折先の振幅分布U2はもとのソースU1のフーリエ変換になっていることがわかる。


ここで二つの例に関して計算を行いどのような回折像が得られるのを検証してみよう。


（１）円形開口

　円形開口の場合回転対称性があるので、極座標表示での計算を行う。



ここでこの回折像を描いてみる。
ｚ＝５００ｍｍ、a＝０．１ｍｍ、λ＝６００ｎｍとする。





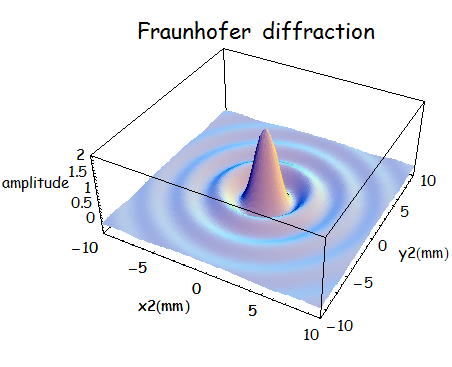
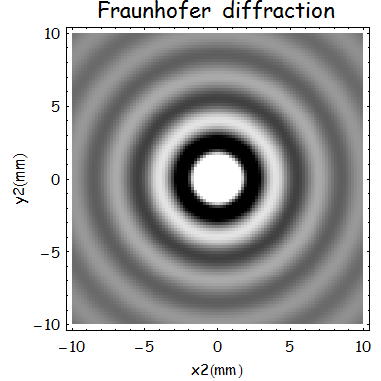
（２）輪帯開口

上式を用いる開口がγa＜r＜aまでの輪帯となっている領域とすると、



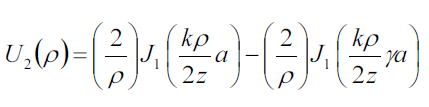
であるので、今回γを0.8、ｚ＝５００ｍｍ、a＝０．１ｍｍ、λ＝６００ｍｍとして計算すると、





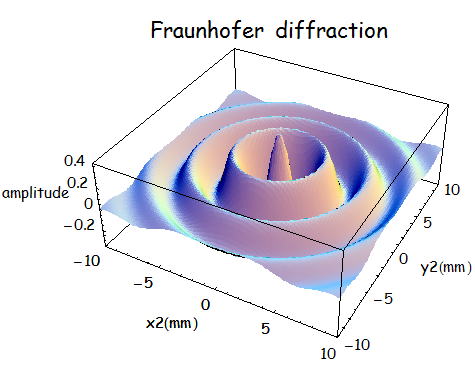
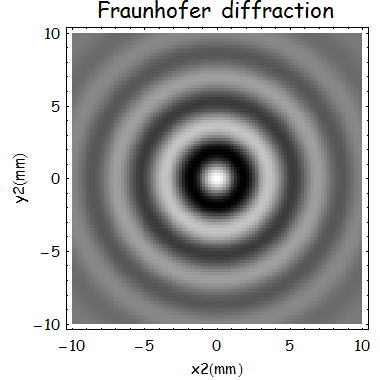
であるので、今回γを0.8、ｚ＝５００ｍｍ、a＝０．１ｍｍ、λ＝３００ｎｍとして計算すると、



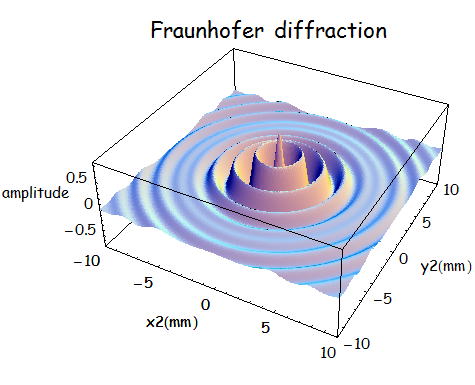
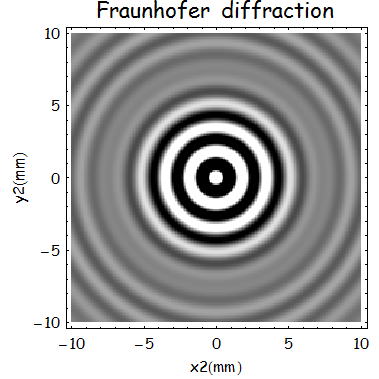
となる。