基本的な回折に関して説明してきたが、薄肉レンズを用いた際にどのような影響が出るのかを考察する。
図に示したように、図では厚肉で透過率も変化しそうだが、今回は薄肉(厚みゼロ、レンズ内の空間的に伝搬量はゼロ)と仮定し、
透過率の変化がなく、波の位相のみを変化させるとする。
その際に、レンズの位相変化(こちらは厚みを仮定して計算)は以下のように計算できる。
座標(x、y)を通過するときの位相変化は
である。その時の位相変化因子は
である。
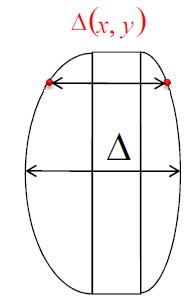
ここで、⊿(x、y)の距離の計算を行う。このとき以下の3つのパーツに分けて計算を行う。
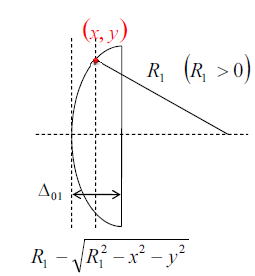
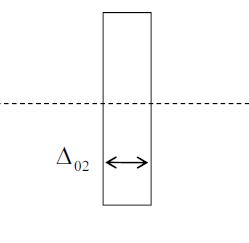
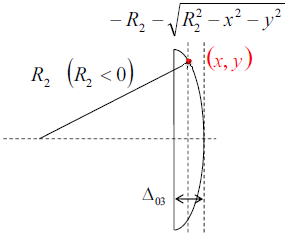
距離⊿(x、y)は以下のように計算ができる
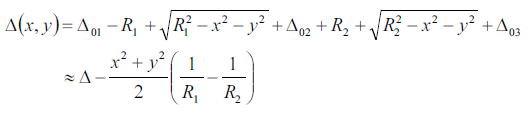
この結果を、先ほどの位相変化因子t(x、y)に代入すると
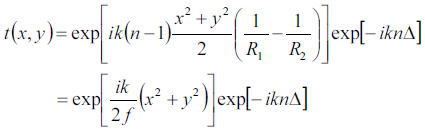
と書ける。
以上の結果から入射波にこの位相変化因子を乗じることで薄肉レンズの効果を取り入れることができる。
ここからは先ほどのフレネル回折の理論とこの節で説明したレンズの効果を取り入れて考えることにする。
回折した光が像を結ぶ先としてZ=fとして計算を行う。
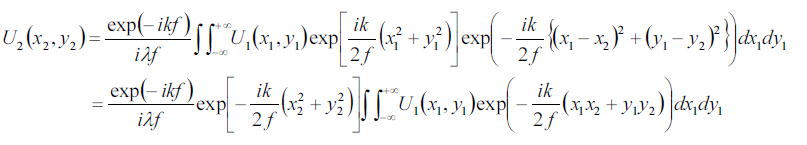
となり、Fraunhoferの近似まで使わなくてもフーリエ変換の形式になり、容易に計算可能となる。
通常はレンズの大きさは有限なのでレンズの瞳関数P(x、y)を導入する。またレンズは基本的に自由曲面レンズでない限り
回転対称をもっているためFourierからBessel変換(前の節で説明した)形式に書くことが可能である。
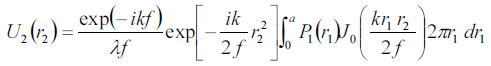
さらに光学系の各種パラメータ設定に依存しない規格化された座標を用いることが便利であることが多い。
そのパラメータをvとして以下のように定義する。
このパラメータを計算結果は省略する。以前の回折の結果と比較するために
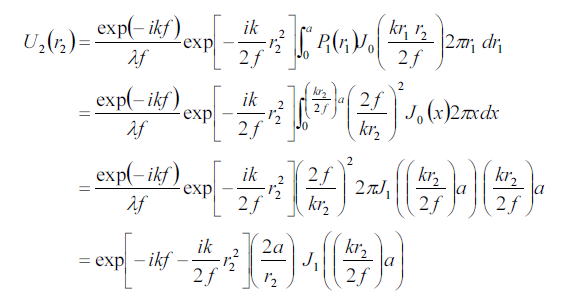
この計算を行う
a=0.1mm、f=500mm、λ=600nm とする。
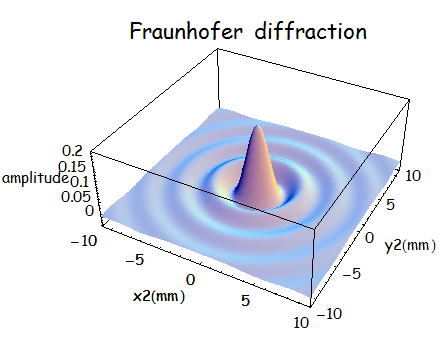
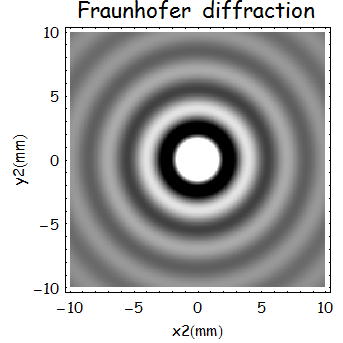
この結果はじつは円形開口でFraunhofer回折理論と得られる結果が同じになる。(実は式も一緒。位相項を除いては)
つまり、レンズを使っても全くスポットが集光できていないことを表している。
レンズの集光効果はどこに行ったのか、レンズでは全く集光できないのかという疑問が生じる。
しかし、この疑問はレンズの口径を大きくとっていないためにほとんどレンズの外側と内側で位相差がついていないと考えられる。
そこで、レンズの口径をフレネル回折が成り立つ範囲まで広げるとする。
a=10mm、f=500mm、λ=600nm とする。
(Fraunhofer回折理論ではこのようなことはできない、前節で述べたようにaを大きくすると回折理論が成り立たなくなるから)
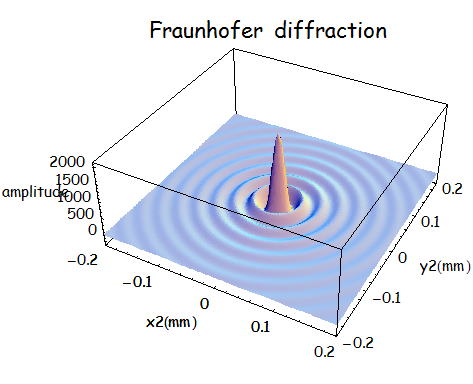
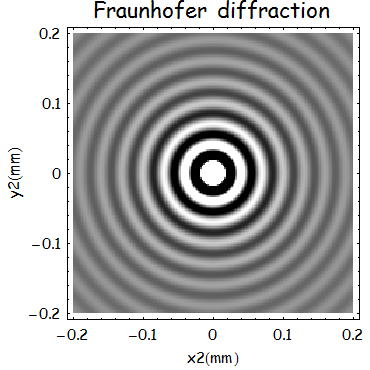
というようにスポットサイズが2ケタ程度小さくなり、レンズでの集光効果があることが分かる。
