
これまで、フレネル回折とレンズ効果や円形開口におけるフラウンホーファー回折に関して議論してきた。
しかしながら、まだ光源分布に関しての議論は行っていない。
回折理論のもとになっているキルヒホッフの回折理論が素元波の重ね合わせと考えるなら、
光源の状態に関してきちんと議論する必要があるだろう。
そこで、光源の状態を考えるわけだが、光源の状態とは何だろうか?
それは二つの状態を考える必要がある。
①光源の強度分布
②光源の位相分布
この2点を考慮する必要がある。じつは今までの議論では光源の状態を空間にわたって一様(強度も位相も一様)であるとして
扱ってきた。このような強度分布と位相分布において相関がある状態をコヒーレント状態(光源)という。
ここでは、それらを含めて考えることにする。
以下の図に示したように単レンズの系を考える。
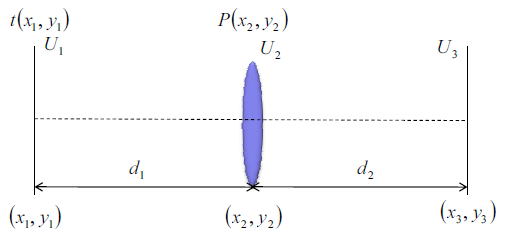
U1の光源から出射した光は、レンズを通過した後の振幅を今まで議論してきたように以下のように記述される。
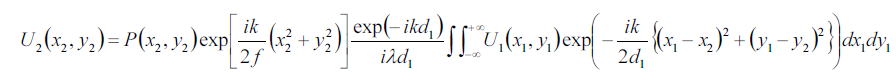
※ここでは、まだ光源の情報をU1に与えていない。
レンズから出射した光は像面x3、y3では、
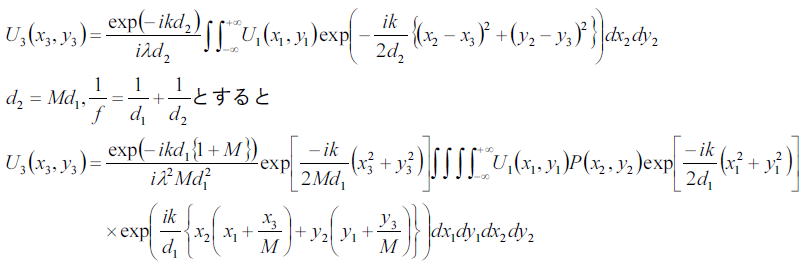
ここで、光源の情報まずは単純なコヒーレント状態である点光源を仮定して記述すると
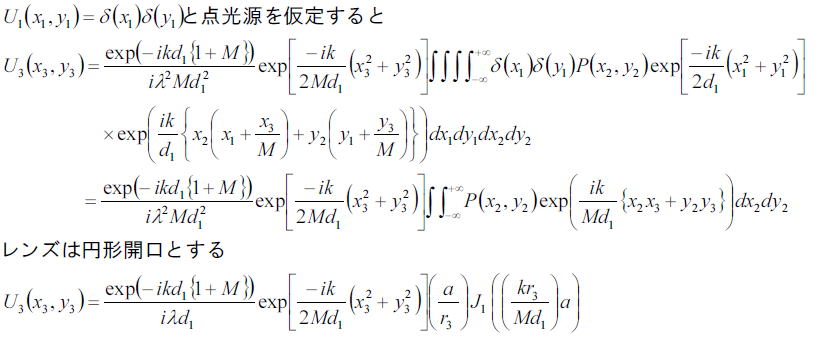
となる。
これ形式、第一種ベッセル関数を像面のr方向で割る振幅は以前に議論したような回折像を
x3、y3面にもたらす。また上式をよく見てみるとr3が倍率Mで割られている。
これは、像面でレンズの効果であるd1=M×d3を反映して、像がM倍になることを意味している。
では、次にもっと一般的な場合を考える。まず光源の状態を考えずに上式の計算を次のように変形する。
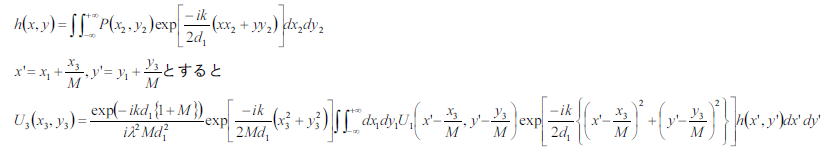
ここで、PSFのhは一般的に(レンズを用いている限り)急峻に変化して(x’、y’)の原点以外では0となる。
そこで、積分の中のexpの項は大きく影響せず、1としていいと仮定すると、
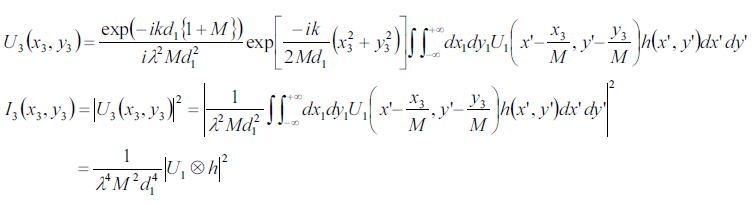
となる。よって、強度は波長の4乗に逆比例しd1の4乗に逆比例し、レンズの倍率の4乗に逆比例することが分かり、さらに
強度分布は、レンズの透過率とレンズのポイントスプレッドファンクション(PSF ; point spread function)点像分布関数との
畳みこみに比例することが分かる
