---

　前節でフォーカスされている像面でのコヒーレント像の考察を行った。ここではさらにその議論を進めてデフォーカス時の観測面での
強度分布の考察を行う。前節では点像強度分布関数ｈにデフォーカスの影響が像面においては消えることを示したが、
今回はその効果が残るため、その時の強度分布を考える。
光学系は、


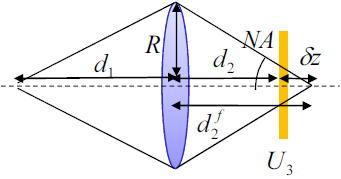
である。このときのレンズからｄ２にある面での強度分布は、前節で議論したように、

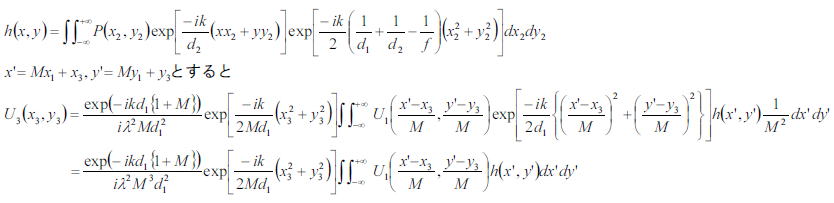
となる。よって、強度分布U3は点像強度分布関数ｈと物体のM倍に拡大した強度分布U1との畳みこみであることが分かる。
ここで、デフォーカスを考えた点像強度分布関数ｈ（ｘ、ｙ）についてもう少し議論する。

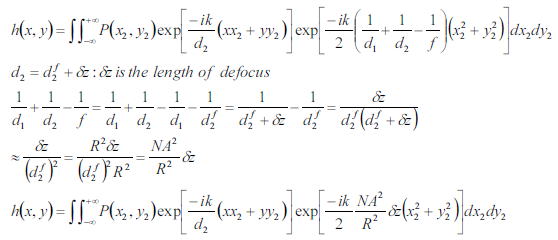
点像強度分布ｈ（ｘ、ｙ）は像側のNAとデフォーカス量δｚを用いて記述することが可能である。



このようにデフォーカスした時の強度分布を表現することができたが、
上式は実空間で表現しており、実際は周波数空間で表現したほうが計算しやすいことが多い。
そのため、これから周波数空間で物事を考えてみる。

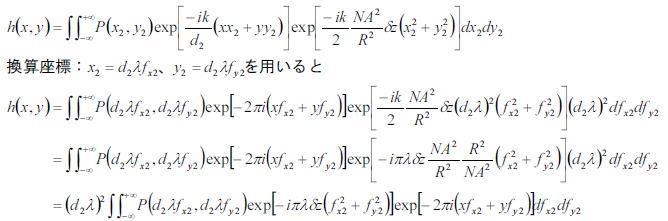
となり、点像強度分布関数は瞳関数とデフォーカスによる位相のExp（二つ目の位相分の積）のフーリエ変換であることが分かる。

ではU3のフーリエ変換を考える

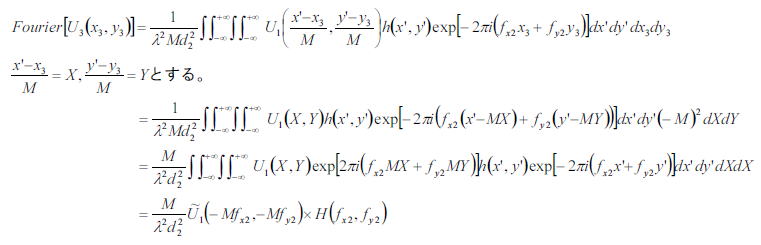
となる。これが意味することは、倍率を考えるとU3の周波数空間においてU1のM倍の空間周波数と点像強度分布関数
のフーリエ成分（OTF(Optical Transfer Function)とよぶ）との積で表現できる。

では実際にどの程度で