---

先ほどの節までで光源をコヒーレント状態で扱ってきた。では光源の空間的にインコヒーレントだった場合どうなるのだろうか？
空間的インコヒーレントとは空間的に強度と位相に関してまったくランダムであり相関がないことである。
このような光源に対して回折像がどのようになるのかを議論する。

以下の先ほどと同じ系；単レンズの系を考える。



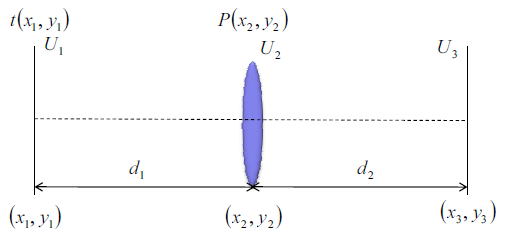
インヒーレントの回折像は実は簡単でほぼコヒーレント光学系で議論したところで答えが導かれている。
インコヒーレントとは空間的に位相と強度に関して相関がないため、U1の光源を点光源に分割し、その点光源がそれぞれ
U3を形成するが強度に変換した後に和をとることを行えばよい。つまり、それぞれの点光源はお互いに独立であるので
U1（ｘ１、ｙ１）とU1（ｘ１’、ｙ１’）がU3（ｘ３、ｙ３）に回折されていったとしても、互いに干渉しないので強度はゼロとなる。
そのため、同じ点光源から発した光でないと干渉しないため、それぞれの点光源U1から作られる強度U3を単純に和をとり
計算を行えばよいのである。



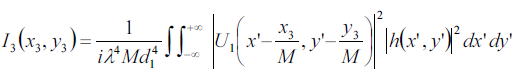
となる


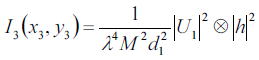
でとなり。コヒーレント結像でのコンボリューションとは多少異なった
光源の振幅ではなく強度でのコンボリューションとして計算される。