この節では、物体は個々の点光源の集まりと考えて像面での結像を考える。
個々の点光源がレンズ系を通過した際に像面でどのような像強度分布になるのかを検討するうえで、
レンズシステムがリニアシステムであることが前提として今後の議論がなされる。
そこで、先にリニアシステムに関して説明する。
①リニアリティ仮定
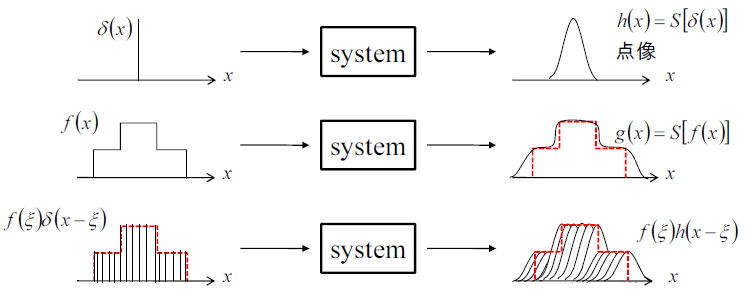
下の図を見ていただきたい。
上段は点光源がシステムに入射したときに、その像が像面でどのようなボケになるのかを示したものである。
点光源が像面でボケて広がった像を点像と呼び、ここではh(x)として表している。
では、実際の光源は点光源ばかりではなく、ある程度の広がりを持っており、関数f(x)とする。
その様子を表しているのが中段である。この光源がシステムに入射するとボケの影響を受けて広がった像g(x)になる。
ではこのg(x)をどのように数学的に表現してあげればよいのだろうか?
それは、まず光源を点光源の集まりとして考える。つまり f(x)=∫f(ξ)δ(x-ξ)dξである。数式2段目。
システムの演算子Sがリニアリティがあるということは、別の言い方をすると重ね合わせの原理が成り立つことを意味する。
つまり、個々の点光源δ(x)の変位の和である変位f(x)はシステムを通った後も、個々の点像S(δ(x))の和である
h(ξ、x)の和でg(x)は表現されると仮定する。f(ξ)は個々の点光源への重みづけである。
(つまり、各光源の強さが異なることを意味している。)
②アイソプラナティズム(シフトインバリアント;シフト不変)仮定
さらに、像形成を数式で取り扱う時に、追加してシフトインバリアント仮定も入れられている。
シフトインバリアントとは、点光源がどの位置にあろうとも、システムを通過した時には、そのボケ方は不変で、
ただ平行移動しただけの形をとることを意味している。
つまり、点像関数h(ξ;x)は実際の数学ではxの位置によって一般的には異なる。
がしかし、点光源がレンズシステムを通過するとき光源の位置(x、y)によらずに点像hは同じであると仮定する。
この点を表現したのが最後の式である。
(ここで紛らわしくて申し訳ないのだが、実際のレンズでは光源の位置すべてにおいて点像hが同じであることはない。
そのため、同じとみなせる範囲内で、つまりシフトインバリアントが成り立つ範囲で計算や評価を行っているのが現実である。)
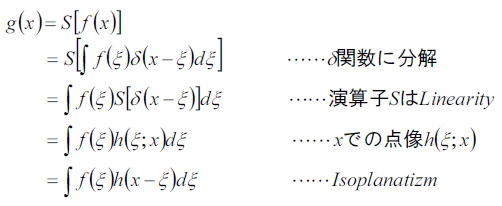
上式を見てみると、数学の得意な人はあることに気づかれると思う。
それは、像g(x)は光源f(x)と点像(ボケ)分布関数h(x)とのコンボリューションになっていることが見てとれる。
よって、像性能を評価する際に光源と点像分布関数を用いて最終的な評価を行うが、
実際にレンズ系の評価で本質的なのは、点像分布関数であることがわかる。
