---

前節では実空間上で点光源をレンズ系を通し、その像を考えた。レンズ系は線形システムであり重ね合わせの原理を仮定した。

また点光源がどのように点光源像がぼけるのかを点像分布関数を用いて表現した。

ここでは、実空間で考えるのではなく、フーリエ空間上で考えたときにどのように考えるのかを見ていこう。

リニアシステムに入った時点光源はボケて点像分布関数となる。

また、矩形波を入れたときは角がなまったような像となる。

では、線形システムにどのような信号を入れたら、もとの関数となるのだろうか？

それは、数学に詳しい人ならよく知っているとおもうが、正弦波が線形システムの固有関数になっているため、

正弦波に関しては振幅と位相のみが異なるだけで関数が変化することがない。


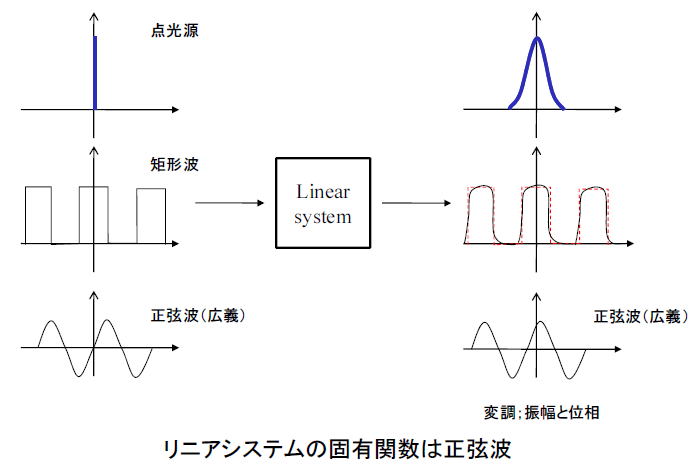
よって、レンズ系（線形システム）を考える際には、固有関数である正弦関数の組み合わせで考えることが一番良い。

というのは、光源を正弦波で考えると位相と振幅の変化だけ見ればよいのだが、他の関数だと上図の中段のように

どのように変化したのか表現が難しくなる。（角の落ち具合がどうとかは非常に表現しづらい）

関数を正弦波で分解する方法としてフーリエ変換という考え方があったのを思い出してほしい。

では、フーリエ空間での光源、点像、像の間で成り立つ関係式を見てみよう。



上式はフーリエ変換を表している。

前節で、光源と点像と像の間にコンボリューションの関係があった。

その式をフーリエ変換すると以下の式となる。



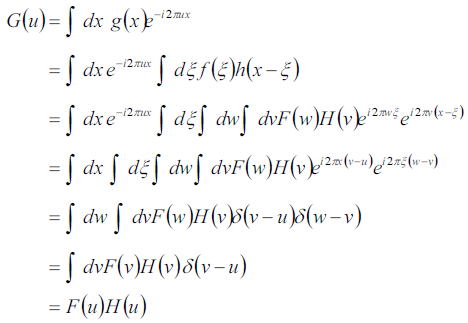
である。

つまり、コンボリューションという複雑な計算をしなくても、フーリエ変換してしまえば（これが面倒と言ってしまうと元も子もないのだが）

光源と点像の単純な積を用いて像を表現することが可能になる。