---

空間周波数において、像と点像と光源の間には積の関係があることを前節では示した。




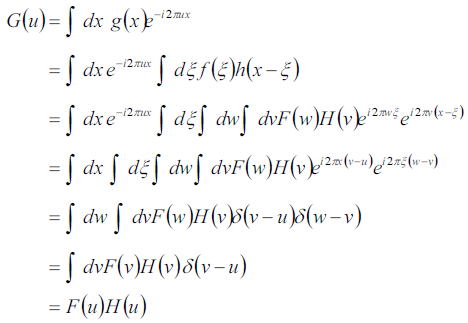
点像ｈ（ｘ）は点光源がどの程度ボケるのかを像面で評価するのに用いられるが、

それをフーリエ変換したH（u）も評価の指標としてOTF（Optical Transfer Function）という伝達関数の名前がつけられている。

OTFの意味を考えると、光源を空間周波数に分解する（ｆ（ｘ）⇒F（ｕ））と

レンズシステムを通過することで点光源が点像ボケｈ（ｘ）の影響を受けたのと同様に、

空間周波数ごとに光源F(ｕ)は、Ｈ（ｕ）の変調を振幅と位相に対して受ける。

レンズシステム通過後の像ｇ（ｘ）を空間周波数ごとに見てあげたものが、Ｇ（ｕ）である。

つまり、点像とは実空間中の点光源のボケとしてとらえていたが、

ＯＴＦは空間周波数で分解された光源をレンズシステムを通過した後に、各周波数ごとどの程度位相と振幅を変化させるのかを

表現したものであり、ＯＴＦと点像はフーリエ変換の関係にある。つまり、ＯＴＦは点像のもう１つの表現である。

根本はレンズシステムが持つ演算子の影響を空間周波数でみるか、実空間で見るかの差でしかない。（どちらも重要である）

いま述べたことが下に示してある。



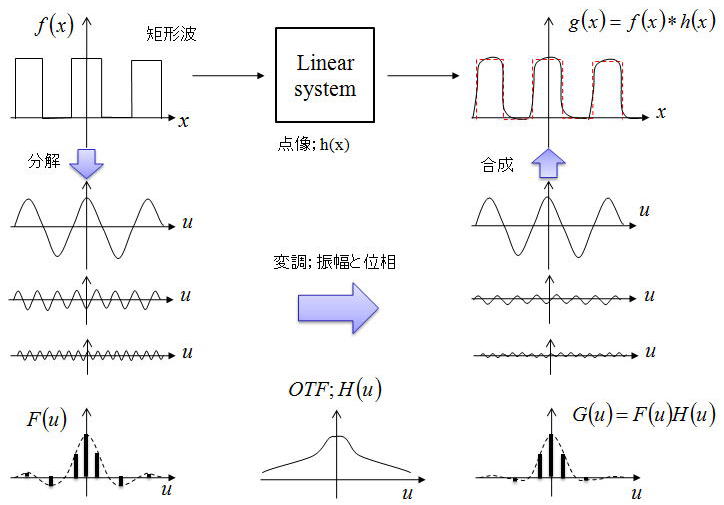
矩形波を持つ光源ｆ（ｘ）が線形システムを通ると点像ボケｈ（ｘ）の影響を受けて像ｇ（ｘ）がひずむ。

上段だけを見ていると、線形システムの影響がどの程度であったのかを理解することはできない。

つまり、他のレンズを持ってきたときに点像ボケが生じるが、

二つのレンズの良しあしがどの程度なのか定量化することが難しいからである。（もちろん像のボケ方を比較する方法もあるだろうが）

そこで光源側ｆ（ｘ）と点像ｈ（ｘ）をフーリエ変換して、個々の空間周波数成分においてＦ（u）がどの程度のシステムの影響を受けるのかを

定量化したのがＯＴＦである。ＯＴＦを見ることによって、今回は低周波数側で振幅が急激に落ちて

高周波数側でなだらかに落ちていくという、さらに進んだ考察が可能となる。

よって二つのレンズを比較する際に２つのレンズのＯＴＦを比較することにより、

どの周波数まで対応できるのか（忠実に再現できるのかを）空間周波数の観点で定量的に比較することが可能となる。

さらに、実空間（点像）だけではイメージできなかったさらに細かなピッチで刻んだ矩形波の像の推定が可能となる。

つまり、さらに細かく刻んだピッチの矩形波は高周波成分での振幅がより大きくため、

ＯＴＦの高周波側の減衰の影響をダイレクトに受ける。

そのため像はもとの矩形波とはだいぶ異なる角がかなり取れた像になるはずだと推定することが可能となる。