---

いよいよ、全体構造のうちの終盤に差し掛かってきまして、

「レンズシステムの点像ｈ（ｘ）ってどう導出するのだよ？」

という問いに答えていこうと思う。

流れとしては、２光束干渉から多光束干渉そして回折積分をし、瞳関数を導入することで点像とはなんぞやに答えようかと思う。

ここで見られる性質として、点像は瞳関数のフーリエ変換であるという事実があるので見ていこうと思う。

もちろん瞳関数とはに関してもね・・・

ではさっそくであるが、まずは２光束干渉に関して考えてみる。



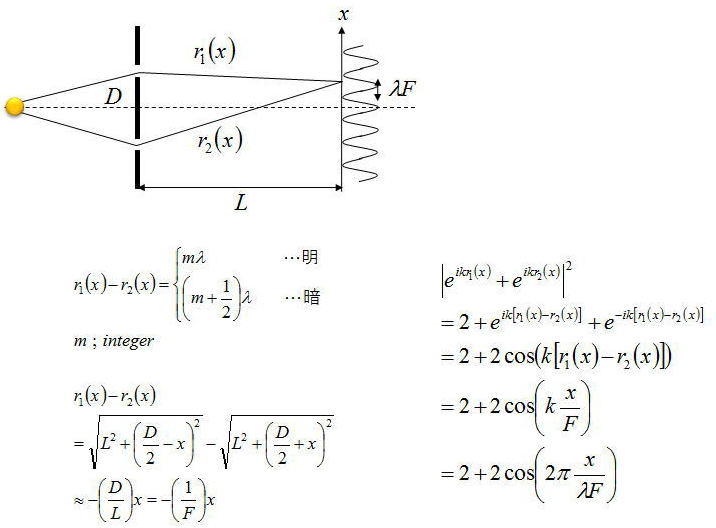
高校物理におなじみの２光束干渉であるが、左の式では高校生でも導出できる式でｒ１−ｒ２の差が波長の整数倍なら強めあい

半波長ずれていたなら弱めあうことを示している。１つの次数差による距離はλF（FはFナンバー）だけ異なる。

右の式は振幅が同じ点光源が重なった時にどのようになるのかを表現したもので、

明暗以外の場所の変化によって、正弦的に変化する振幅強度も表せている。

こちらも当たり前だが、１つの次数差による距離はλFだけ異なる。



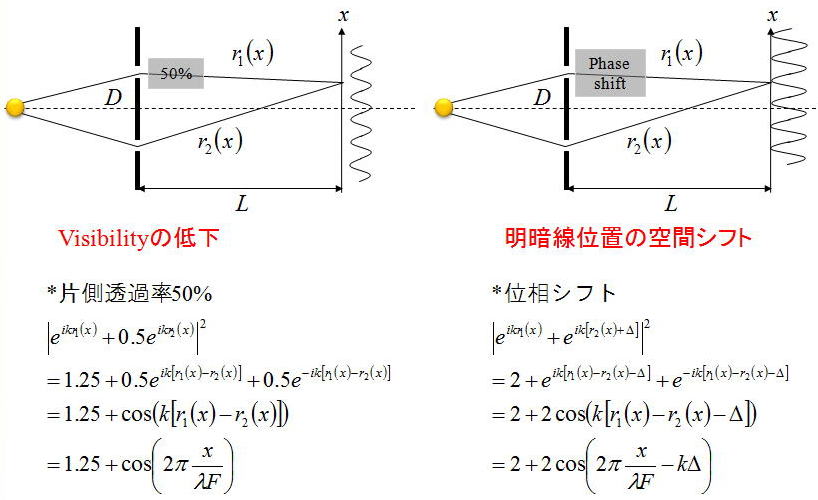
上記は２光束干渉の変形版である。高校生に多少敷居が高いが、片側の開口に透過率５０％を入れた場合（左）と、

位相シフターを入れた場合（右）で干渉縞がどのように変化するのかを考察をする。

透過率５０％の場合だと結果は、Visibilityの低下を招くことを示唆している。

つまり、干渉縞の明暗の境界がはっきりしなくなることを意味する。

次に、位相シフターを挿入した場合には、Visibilityの低下はないが、干渉縞の空間的なシフトが発生する。

以上のことから２光束干渉に関してのいくつかの例をあげながら見てきた。

このような議論は３光束、４光束でもおこなえるが、多少はなしが複雑になるので、

次の節では２光束干渉から一気に多光束の干渉を考えてもよいかと思う