さて、多光束干渉を考えて回折積分に話を進めていこう
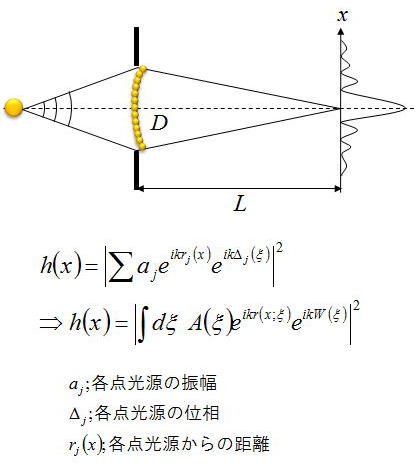
上図が開口をいくつもの点光源とみなして、Lだけ離れた面での干渉を考えたものである。
2光束干渉と同様にすべての点からの点光源exp(ikr)に対して、振幅aj と 位相⊿j を追加拡張して考えて
重ね合わせたものである。(これが多光束干渉である)
ここで、点光源を無数に考えて積分系に持っていったものが回折積分で下式ように置き換わる。
回折積分まで来たが、ここまででは御利益が何なのかわからない。
そこで、以下の瞳関数P(ξ)と、点像強度h(x)の点像振幅v(x)を導入して議論をする。
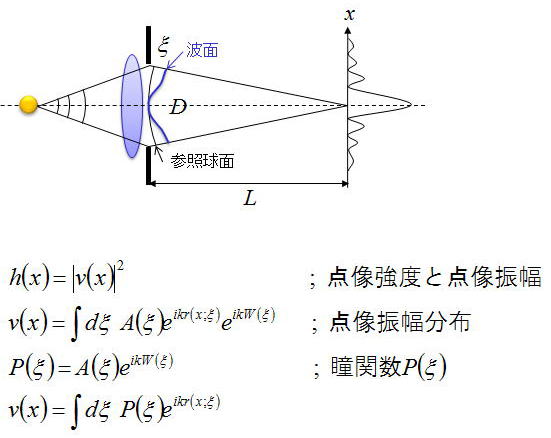
導入した点像振幅v(x)は瞳関数P(ξ)を用いて表現している。
瞳関数とは式の示しているように、瞳の各点光源の振幅成分と位相ずれ成分の積をとったものである。
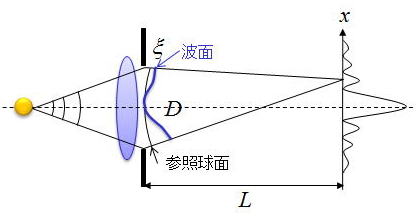
点像振幅v(x)は参照球面波からのずれととらえなおして位相項をexp(ikW’(ξ))と取り直す。
参照球面波からのずれと考えるのは、球面波が理想的な点光源(理想的なボケ)になるためなので、
参照球面波を基準としてその差分を波面収差(波面のずれ)と考えることで、
点光源の結像ボケ、つまり、点像振幅v(x)を評価しようという考えである。
ここで問題になるのが、光軸に集光する、つまりx=0に集光する波面とxが光軸からずれた所に集光する波面とで
波面収差の表現の仕方が異なるという点にある。
それは、集光点が違う波の進む方向が異なるところからくる波面収差量の差を表現してあげる必要がある。
よって、x=0に集光する波面をW(ξ)(*紛らわしいがすでに上の式のW(ξ)とは別物)としたときに、
x点に集光する波面はx/L=tanθだけ傾いているために、それだけ傾いた波面収差を付加する必要がある

よってそれを用いて、さらに、瞳関数を用いて計算すると、
点像振幅v(x)は瞳関数P(ξ)をフーリエ変換している式となっている。
