はじめに

　　電気回路を考える際に重要な点は、この問題を人間が扱う際にどこまで表現を抽象化するべきなのかと

いう点にある。つまり、電気回路の問題を解くには、電流、電圧の解を求めることであるから、ミクロな点で考

えれば、大学の初年度で習うようなマクスウェルの方程式で、電子の動きを求めることができるはずである。

しかし、そこまでミクロに考えなくても、マクロ的な視点で解くことができるのが、電気回路での法則である。本

ページでは、それらの諸法則に関して簡単にまとめ、電気現象をどこまで抽象化されたレベルで（マクスウ

ェルの方程式でない）表現していくのかに関して応用も含めて考えていきたいと思う。




電気回路における仮定

電気回路では、電磁気学と決定的に異なる前提を設けている。

電磁気学では、電子に影響を与える電磁波は光のスピード、つまり、伝達速度は有限である。

ところが、電気回路の場合に関しては、電子回路の長さ程度の場合は光のスピードは一瞬なので、端子間で

電圧がかかった際に、端子の両端で同時刻に同電流量が流れる。要は、電磁場（電圧）の時間の伝わりは

考えないとすることを仮定している。


電圧と電流の関係


電気回路では、電圧と電流が必ずペアで頻繁に出てくる。
　　　　　　　　
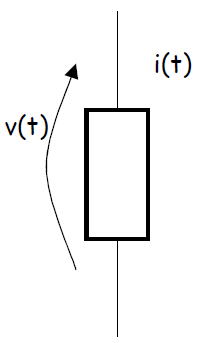
電圧と電流の正の向きは、逆向きに定義するのが普通である。（というのは、素子を通過するときには電圧

は降下するのでこうとっておくほうが結果として得られる符号は正のままでいい。）

また、電圧は電圧の間だけで成り立つ法則がある。

電流についても電流の間で成り立つ法則がある。

後で説明するように回路素子の電気的特性は電圧と電流の結びつける働きをする。

（簡単なのは、抵抗の法則であるv=iRなどが電流と電圧を結びつける。）


キルヒホッフの電圧法則


電圧は回路中の閉回路を一周すると、（電子がもっているエネルギーは）元の値に戻っているはずである。

よって、次の法則がなりたつ。

　　　　　回路のループに沿った電圧の代数和はゼロ。
　　　　　　　　　　　　　　　　　　　　（キルヒホッフの電圧則）

このことを別の言い方をすると、つまり回路中で電子が持っているエネルギーは、いろいろな素子を通るにつ

れて変化するが、元の回路中の位置に戻ってきたときには同じ電子のエネルギーを持っているはずである。

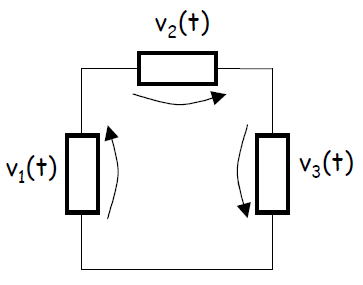
　例えば、下の図を例にしてこの法則について説明する。

この閉回路に成り立つ式に関して説明する。

　　　　　　　　　　　　　　　　　　　　　　　　v1(t)+v2(t)+v3(t)=0

という式が必ず成り立つ。

つまり電位の変化の和は一周してきたらゼロになるという法則である。




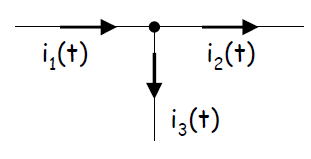
キルヒホッフの電流法則


電流とは電子の流れである。それがどの程度流れるかを定量的に表したものが電流量であるが、電流にお

いても以下の法則が成り立つ。

　　　　回路中の各節点（合流点）における電流の代数和はゼロ。

ここでの、符号は電流が合流点で入るときに正で、出て行く際に負にするか、もしくはその逆を考えている。

ここでも、例を出すとすると
　　　　　　　　　　　　　　　　　　　　　　　　i1(t)-i2(t)-i3(t)=0
となる。
この式を変形すると、
　　　　　　　　　　　　　　　　　　　　　　　　i1(t)=i2(t)+i3(t)

となり、i1の電流はi2とi3の和である。つまり、電流の流れは保存することを意味している。