---

この説では今まで議論してきたFourier光学を応用して顕微鏡に関する議論を行っていく。
まず、下に示したような系を考える。
点光源から出た光はレンズでサンプル上に集光されそのあと無限大に広がったディテクタに強度を検出される系であるとする。
今回ディテクタからサンプル面とサンプル面からレンズの距離は同じとする。




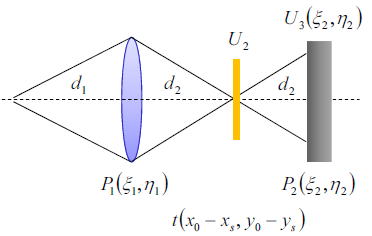
光源が点光源と仮定すると、Coherent Imagingで議論したと同様に、サンプル面での振幅U2は、




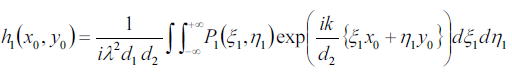
と記述することができる。
さらに、サンプル面での透過率や位相変化をｔ（x0、y0)で記述することにする。
また顕微鏡ではサンプルに照明する領域を移動させる機構があるが、今回はサンプル面が移動するとして、
その移動量を（ｘｓ、ｙｓ）と書くことにする。
無限大のディテクタ上に作る像は、（位相成分は無視することにして）
P2はディテクタの感度となる。


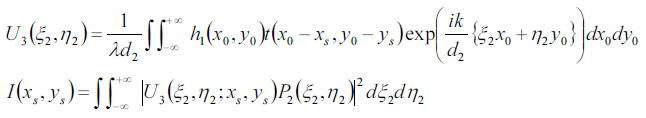
となる。上式を整理すると、

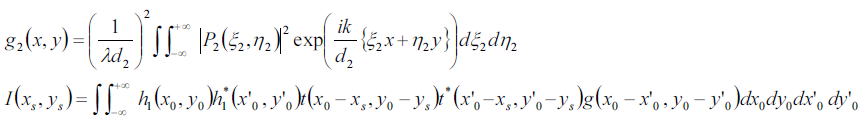
となる。

ここで、P2に関して基本的にはディテクタの感度は全体にわたって均一であると仮定すると、
ｇ２はδ関数になる。そのため、

とｈ１とｔは畳みこみを用いた形式で書くことが可能である。
つまり、これはインコヒーレント光源で議論した像と同じとなる。

さらに、P2が極限に小さいディテクタであると仮定すると、

となり、これはコヒーレント光源で議論した像と同じとなる。

しかしながら、実際はこのように単純にコヒーレントとなるかインコヒーレントになるとか区別できるわけではなく
ここでは議論しないが部分的にコヒーレントであることが一般的である。