---

伝達関数の導出

この節ではrough surfaceに対して、ピンホールでの像は以下の式で記述される。
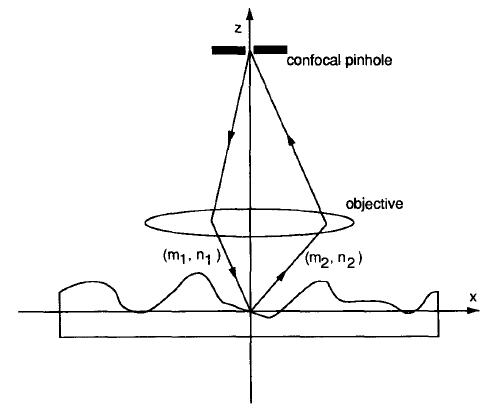
ここで、ｍ、ｎは下の図に示している方向余弦である。
P1、P2はそれぞれ入射と出射の瞳関数である。





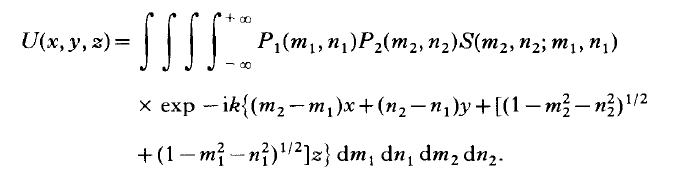
ここで、ｍ、ｎ、ｓを以下のように定義するとピンホールでの像Uは次のように表現される。
ここで注意したいのはKirchhoff近似が成り立つ条件ではscattering function　Sは４つの変数から３つの変数にすることができる。



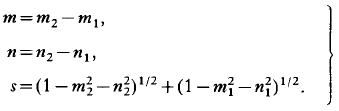
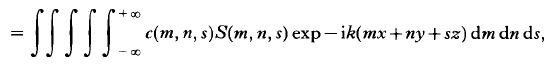
ここで、ｃは伝達関数で、



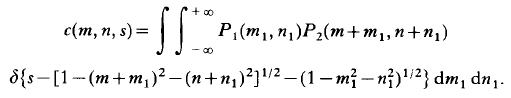
伝達関数 : c(l,s) の計算

収差がまったくない（Abberation free)ならば、
伝達関数の計算は二つの瞳関数の共通部分体積、つまり二つの球体の共通部分の体積を求めることと同じになる。
ここではそのような条件下での計算を考える。
通常のレンズを用いる限りでは1軸、光軸の回転対称性があるから、



と定義して、瞳のNA（numerical aperture）をsinαで表すと伝達関数は、以下のように分類される。


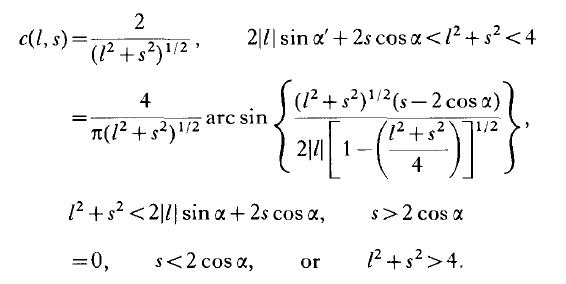
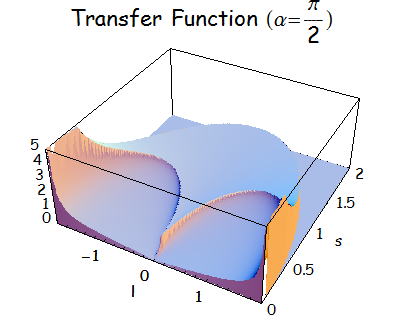
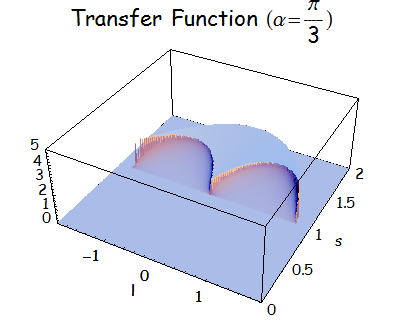
上式に関して図示してみる。




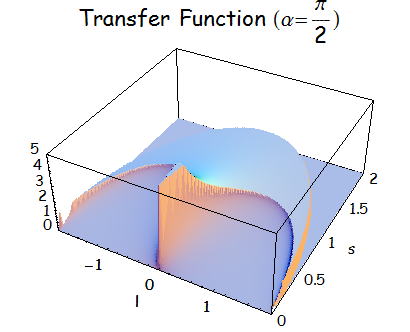
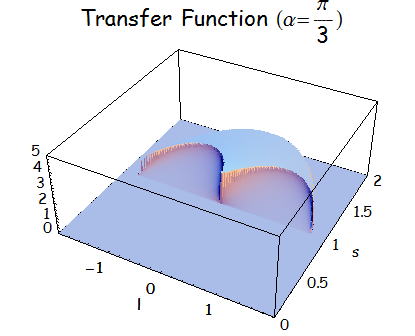
伝達関数 : c(l,s)×S(l,s) の計算

　キルヒホッフ近似でscattering function S(l,s)に関しては以下の式で表現される



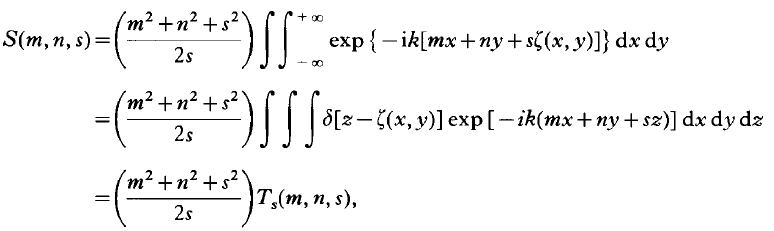
この式と先ほど求めた伝達関数C（ｌ、ｓ）の積を考える。NAが小さい開口しかない場合Ts（ｌ、ｓ）は１とみなすことが可能である
そこで今回は計算例としてその場合を考える。