

データの中の小さな変化に気づけることは非常に大事なスキルです。
大きなピークの肩に小さなピークがある場合、つまり、ピークどうしが重なりあったケースで
どのようにピークを浮き上がらせることが出来るだろうか?ピーク分離方法の代表的な方法は、
ピーク分離方法
- スペクトルの微分
- フーリエセルフデコンボリューション
スペクトルを微分するとどんな良いことあるのか?
- ピークの半値幅を狭めて、大きいピークのそばにある識別しにくい小さなピークの位置を明確にする
- ベースラインを平坦にする
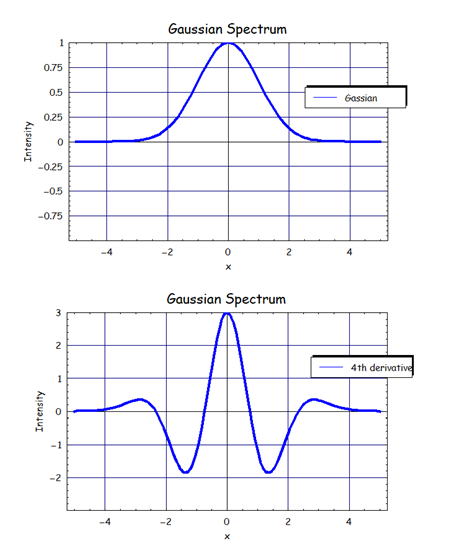
下のグラフを見てみよう。上のグラフはガウス関数で、下のグラフはその4次の微分である。
微分することによりスペクトルの幅が小さくなることが分かる。
そのことにより二つの隣接したピークを分離することが可能になる。一方、その代わりに裾に偽ピークが出現し
真のピークと間違わないようにすることが重要になる。
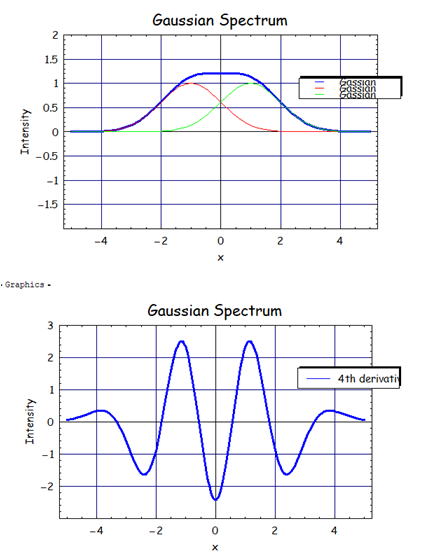
複数のピークが重なってそれぞれのピークが見えないときの微分の効果は?
では次に複数のピークが重なってそのままの信号ではそれぞれのピークが見えないときに微分の効果は
得られるのかどうか実際に確かめてみよう。まず上のグラフは先ほど用いたガウス関数を並行シフトして
その和を計算したものである。下のグラフはそれを4次微分した結果である。見てわかるように、
微分する前はそれぞれピークがあるようには見えなかった信号が、4次の微分をすることで
2つのピークが明確に現れたことが見て取れるだろう。
実際には、微分アルゴリズムはSavizky-Golay法が一般的には知られており、デジタルデータを微分したり
スムージングしたりする際に最も多く利用されている方法である。
1) Savitzky. A, Golay. M.J.E, Analytical Chemistry 36, (8), 1627?39, (1964).
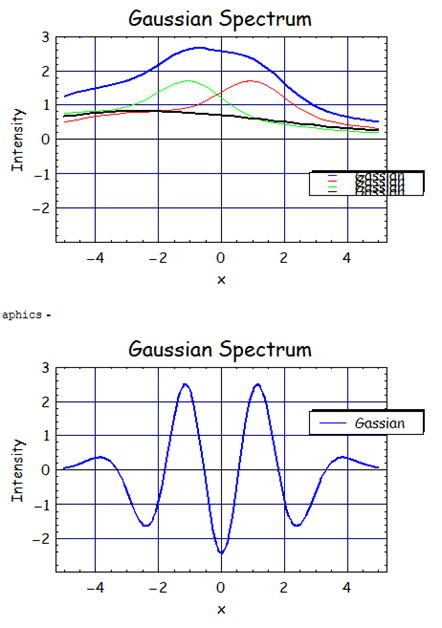
次にベースラインを平坦にする効果があるかどうかを確かめてみよう。
次に示している上のグラフの黒実線ようにベースラインを付加したスペクトルに対して微分してみよう。
微分した結果は下の図になるが、先ほどの微分した結果と同じスペクトルが得られ低次のベースラインの
スペクトルの影響は微分したスペクトルには現れないことが分かる。
いったん整理すると、
- 微分スペクトル
微分処理を加えたスペクトルのこと。1次微分, 2次微分が使われることが多い。まれに 4次微分以上の高次微分が使われることもある。 - 2 次微分スペクトル
2次微分処理を加えたスペクトルのこと。 - ピークトップは負の数になるので、定量する際は一般的に正負の符号を反転させる。
- ゼロクロシングポイント
微分スペクトルが縦軸の0点と交差する点
