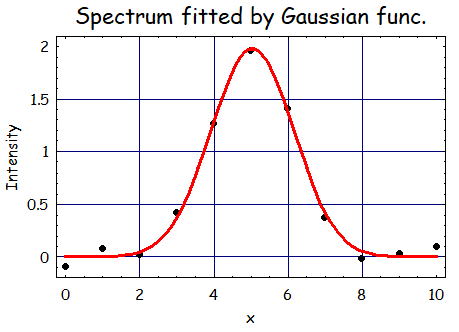
---

　　

　次にピーク検出としてGaussianフィットしたときにどうなるのか見てみよう。

ガウス関数とは



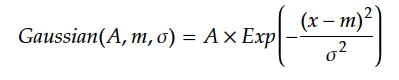
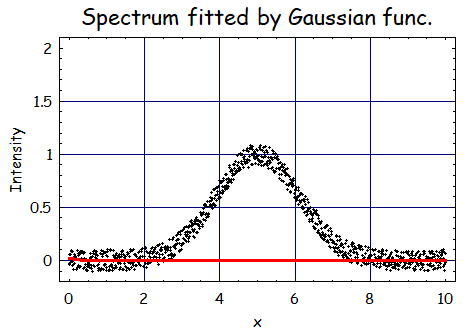
という関数であり、以下の例は、A＝２，ｍ＝5、σ＝1で、それをΔｘ＝0.01ピッチで振幅Δｙ＝　-0.1〜0.1

のランダムノイズを付加して生成したガウス関数に倣うデータをガウス関数でフィットした結果である。

下の図からも分かるように十分にガウス関数が目視で確認できるレベルで十分にデータ点数がある場合は

容易にガウス関数でフィット出来ていることが分かる。




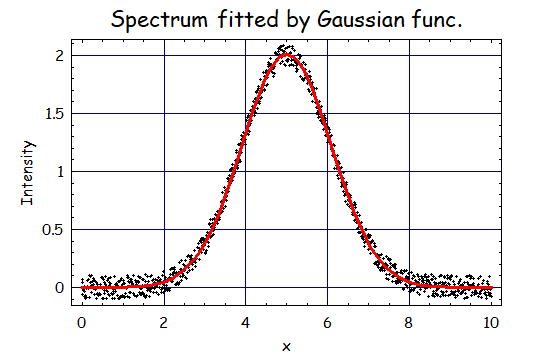
1.データ点数を変えた場合

次にデータ点数を1/10にしてみよう。この場合でも安定して結果が得られている。




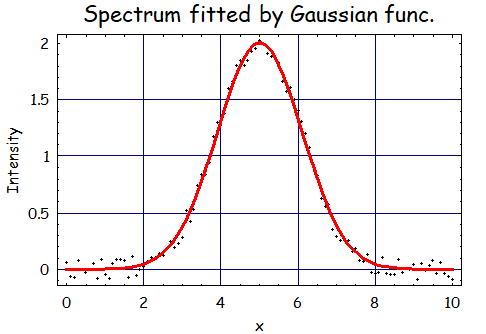
ではさらに1/10のデータにしてみると、とフィッティングに失敗するケースが散見される。

ここからパラメータがA,m,σ全てがパラメータであるとき、ある程度のデータ点数が必要となることが分かる。



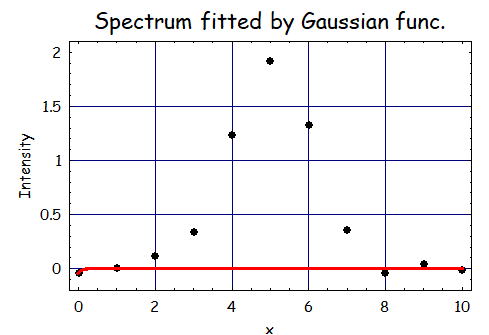
2.ピーク値を変えてみた場合

振幅を半分にしてみるとフィッティングの結果は失敗している。全パラメータを振った場合

振幅も重要なパラメータの一つになっており、それが小さいとフィッティングで正しい解を見つけるのが難しい。



3.ピークのｘの初期値位置を指定して、データ点数を減らしてみた場合

初期位置ｘを5にしたときに先ほどデータ点数、1/100倍にして、つまり、Δｘ＝1あたりに1点プロットする

とした際にきちんとガウスフィット出来るかどうか検討した。

先ほどとはうってかわってきちんとフィッティングが安定的に出来ている。

しかも結果はA -> 1.95053, ｍ -> 4.97217, σ -> 1.10988

であるので、ノイズを与える前の元のガウス関数に近い結果が得られているのが分かる。

ここではグラフで表さないが半値幅に２〜３点くらいあれば良いフィッティング出来ることが分かった。