

Background推定法として、Whittaker Smootherを利用した推定法であるAsymmetric Least Squares
Smoothing(ALS)がある。
Asymmetric Least Squares Smoothingの原理
単純移動平均を利用したBackground推定では、元データと単純移動平均をとったデータを比較し、
値の小さい方を採用する方法をとっていますが、ASL法では重みwiを活用します。
計算フロー
- 大きなλを与えて、Whittaker Smootherを適用する。その時の重みは全て1とする。
- 元データと比較し、yi>ziとなる点の重みをパラメータpとし、そうでない点は1−pとする。
- 再びWhittaker Smootherを適用する
- 再度、2の処理を実行し、全ての重みwiが変化しなくなるまで繰り返す。
計算フロー1のWhittaker Smootherにおいて重み1かつλをかなり大きくすることは、
前節で見たように低高周波のノイズが取れて、かなりなめらかな信号が得られることを意味する。
しかし、信号全体はなめらかになっているが、
ピークがある場所を完全に無くせてなくBackGroundだけの信号になっていない。
そこで、計算フローの2−4を行うことになる。
Whittaker Smootherの式は、
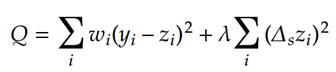
であり、このQを最小化する意味は、重みwiが大きいと元データ値との差が小さくなるようになり、
一方、wiが小さいと近傍データとのずれΔziが小さくなる、つまり、滑らかな曲線になることを重要視する。
この特性を利用すると、
yi(元データの値)>zi(滑らかなWhittaker推定値)となる点(i)は、
BackGroundレベルの値でなく、まだピーク信号があると解釈できる為、
小さい重みpを与えることでよりデータを滑らかにさせる処理を行わせます。
一方で、BackGroundに近い点、つまり、yi<ziの点に関しては、大きな重み1−pを与えることで、
元データに近い値、つまり、BackGroundデータに近づかせる。
重みwiが変わらなくなるまでこの計算フローの2−4を繰り返すことで、
全体データ点はベースラインに近い滑らかな曲線にすることができる。
重みの掛かり方が各データ点に対してAsymmetryなのでこの名称がついていると思われる。
Eilersによると0.001<p<0.1がよく、またλに関しては、10^2<λ<10^9がよいとも述べている。
では実際にデータ処理を行いその結果を見てみよう。
1.S=2、λ=10^2、p=0.1の時
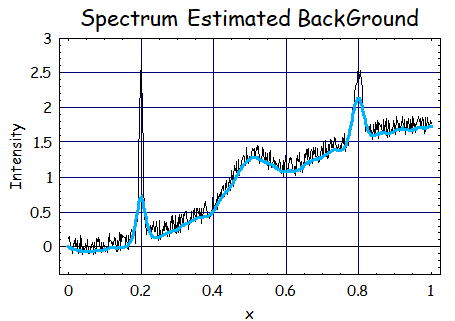
λの値が比較的に小さく、pの値が大きい場合の結果を見てみると、
推定したBackGroundは十分にノイズが平滑化されているように見えるが、ピークの値に沿っている為
BackGroundの推定がきちんと出来ているとはいえない。
これは、Whittaker Smootherの特性であるλの値が大きいと十分にピーク信号を消せていないところが現われている。
2.S=2、λ=10^6、p=0.1の時
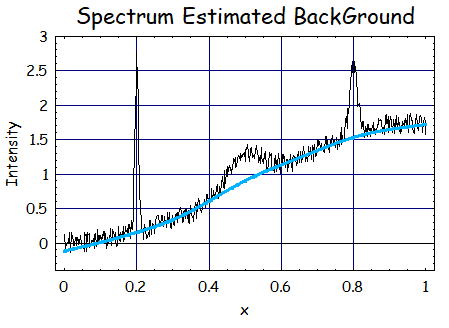
次にλをさらに大きくした際の結果を示す。前のと比べるとかなりベースラインに近づいたように見える。
この時点でかなり良いBackGroundの推定が出来ているように思える。
3.S=2、λ=10^8、p=0.1の時
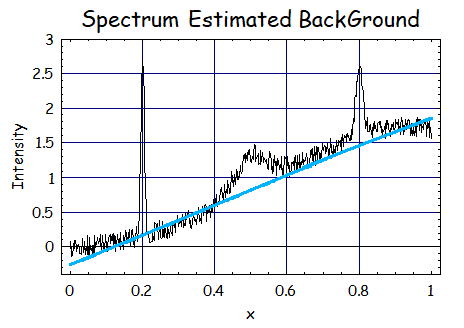
λをさらに大きくすると、今度は推定BackGroundが直線的になっており、うまくBackGround推定が出来ていない為、
λは先ほど程度にとどめておいた方が良いことがわかる。次に重みpに関して調整してみよう。
4.S=2、λ=10^6、p=0.005の時
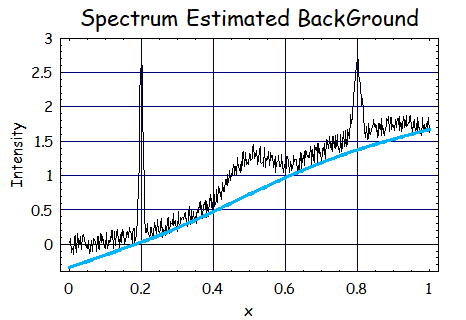
重みpを0.005まで小さくするとこれもBackGroundから若干ずれており、
収束先が実際のB.G.より下になってしまっているし、推定したB.G.もやや直線的である。
5.S=2、λ=10^6、p=0.05の時
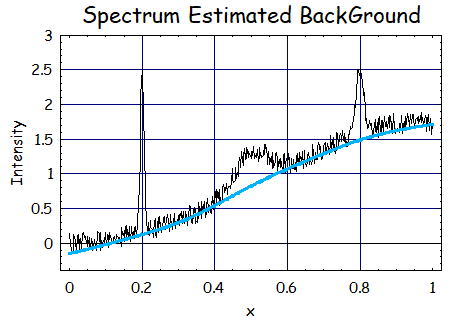
最終的にλの値とpの値を主観的に決めているが、かなり、実際の信号のB.G.とAsSL法で推定したB.G.は
かなり良い近似になっていると思う。このように最初にデータを推定するのはパラメータを変更する必要があるので
大変である。最後にB.G.が変わった時に上記のパラメータでいいのかどうか確認してみよう。
6.S=2、λ=10^6、p=0.05の時
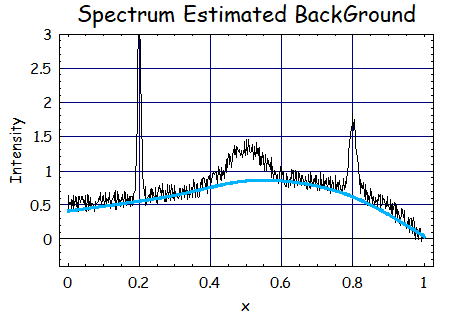
B.G.の特性を変更した結果が上のグラフになる。
この時先ほどうまくいっていたλ=10^6でp=0.05でもうまくB.G.が推定できている。
今回ある程度B.G.を変えてみたがこの範囲では再度パラメータを調整しなくても、B.G.の推定はうまくいっている
ように見える。どういった場合にこのパラメータが破綻してくるのかはもう少し検証が必要である。
