---

　　

　信号処理に元のデータに重みづけをして足し合わせていくという、フィルタを掛ける方法がある。

これは前節で説明したように単純にΔｘを動かしながらウィンドウ幅分足し合わせていくのとは少し異なる。

ここでの考え方はフィルター関数ｆ（ｘ）というものを用意して、

Ｆｉｌｔｅｒｅｄ＿ｙ（ｘ）＝ΣData（ｘ＋ｎΔｘ）×ｆ（ｎΔｘ）

という重み関数（フィルター関数）を考える。この式は移動平均のようにData（ｘ+ｎΔｘ）を足し合わせていくのではなく

重み関数をかけている点に特徴がある。では具体的にみていこう。

まず、元データとしてガウス関数のデータを今までと同様に用意する。ガウス関数とは、



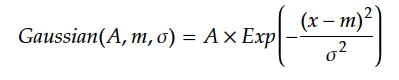
という関数であり、以下の例では、A＝0.２，ｍ＝０．５、σ＝０．０１で、それをΔｘ＝0.00２ピッチで振幅Δｙ＝　-0.15〜0.15

のランダムノイズを付加して生成したガウス関数に倣うデータを生成する。

次にさらに、ガウスフィルタで、A＝1/√（２πσ）、ｍ＝0、σ＝（可変）のフィルタ関数ｆ（ｘ）のガウス関数のフィルタを用いる。

そして、そのデータをガウス関数でフィットすることを考えて、十分に元のA,m,σに近いパラーメータを持つ

ガウス関数となるかを確認する。

１．ガウスフィルタのσ＝５のとき


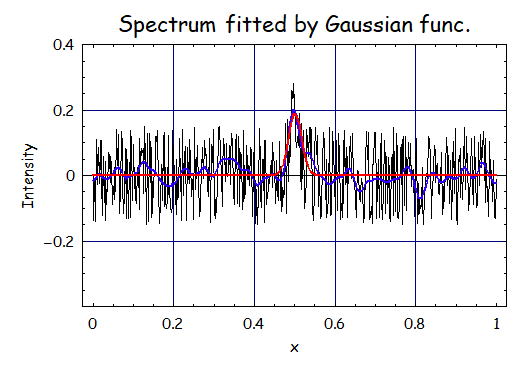
で、フィッティングの結果は、A＝0.19、ｍ＝0.50、σ＝0.017である。

これを見てるとGaussianフィルタをかけることによって得られる信号（青線）は、ノイズ成分が低減されている。

一方で隠れていたガウス信号とノイズの信号とを識別するのは難しい。ｘ＝0.5以外の場所でも信号があるように見える。

２．ガウスフィルタのσ＝2.5のとき



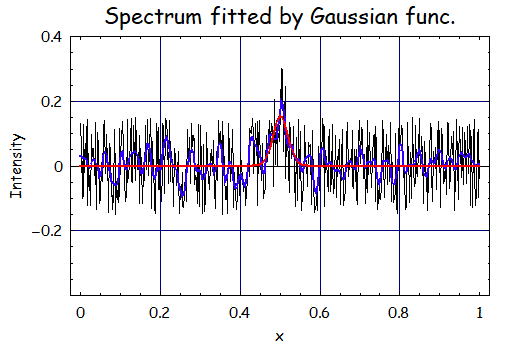
で、フィッティングの結果は、A＝0.15、ｍ＝0.50、σ＝0.019である。

フィルタのガウスのσを小さくすると元信号のσの幅とフィルタでかけてノイズの広がりが同程度になっているのが

見て取れる。ゆえにガウス信号とノイズにフィルタをかけた後のノイズのスペクトル幅がかなり同程度になっている。

結果として二つの信号の区別がつきづらいのがわかる。

事実、このフィルタのσが2.5の時はガウスフィッティングの結果も安定しなかった。


３．ガウスフィルタのσ＝1のとき



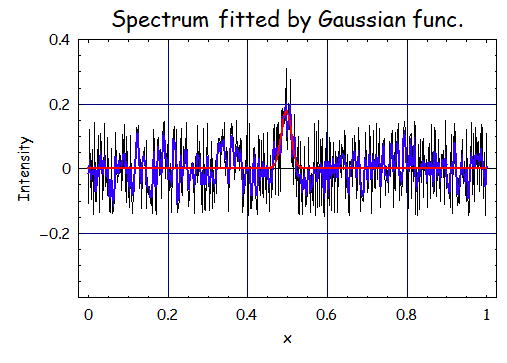
で、フィッティングの結果は、A＝0.18、ｍ＝0.50、σ＝0.013である。

フィルタをかけた後、今回のガウスフィルタのσの幅は狭いので高周波成分しか平滑化されていない。

このように見てきたように、ガウスフィルタのσを変更することでどのくらいの周波数までのノイズを平滑化したいか

をコントロールすることが出来る。