---

　　

　信号処理に移動平均（Moving Average）という考え方がある。

移動平均はｘ方向にΔｘ動かしながらｙデータを足していく。具体的には、Δｘを10回分動かして足す場合、

ｙ（ｘ）、ｙ（ｘ+Δｘ）、、、、、ｙ（ｘ+10Δｘ）の全ての和を取り10で割ることを行う。

今回はその状態を確認するに当たって、ガウス関数にノイズを加えて、移動平均の効果を見ていくことにする。

ガウス関数とは、



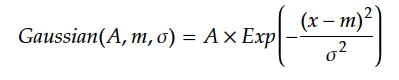
という関数であり、以下の例では、A＝0.1，ｍ＝5、σ＝1.1で、それをΔｘ＝0.01ピッチで振幅Δｙ＝　-0.5〜0.5

のランダムノイズを付加して生成したガウス関数に倣うデータを生成する。

そして、そのデータをガウス関数でフィットすることを考えて、十分に元のA,m,σに近いパラーメータを持つ

ガウス関数となるかを確認する。

１．移動平均が１、つまり何も移動平均しない場合


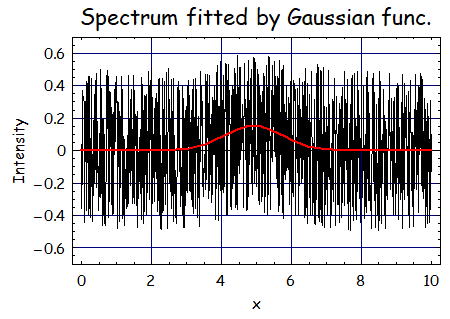
で、フィッティングの結果は、A＝0.15、ｍ＝4.91、σ＝0.83である。

この場合、データをみると薄っすらガウスのピークがあるように思うが明瞭には見えない。

しかしながら、フィッティングした結果、ノイズに信号が埋もれていても

元のガウスパラメータと概ね同程度のガウス関数のパラメータが得られていることが分かる。


２．移動平均が５である場合



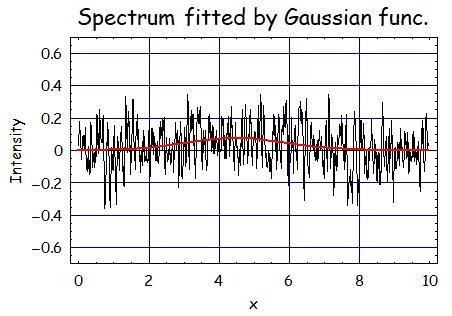
で、フィッティングの結果は、A＝0.076、ｍ＝4.52、σ＝1.46である。

移動平均してノイズの量はかなり減ったが、データ点数も同時に減らしている為、

信号があるように見えなくなっている。

その為移動平均する前と比較してより信号がノイズに埋もれているように見える。

実際のパラメータも先ほどと比較して振幅が減り、中心位置や幅も本来の値からはずれている。

３．移動平均が１５である場合


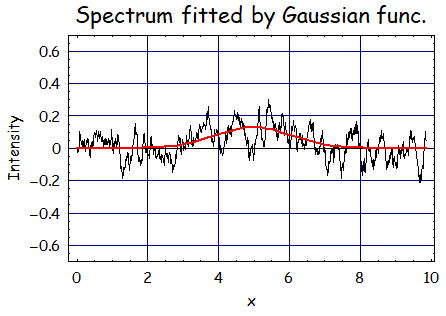
で、フィッティングの結果は、A＝0.129、ｍ＝4.98、σ＝1.08である。

今回の結果はノイズの量もさらに減り、同時にデータ点数も減っているが信号があるように見える。

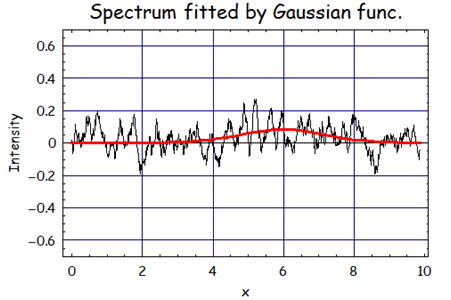
再度計算を回した結果が右になる。データ点数が少ないために平均化後ピークの位置が右に寄っている。

その為に、A＝0.08292、ｍ＝5.99、σ＝1.178となり、特にピーク位置のずれが大きいことが分かる。

これを回避するためにはどうすればいいかというと、単純にデータ点数を増やすことにある。

４．移動平均が１５で、元のデータ点数に対して15倍のデータ点数にした場合


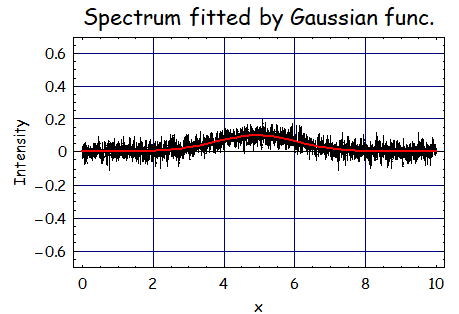
で、フィッティングの結果は、A＝0.0994、ｍ＝4.92、σ＝1.16である。

移動平均が１５であるにもかかわらず、データ点数が十分に多いためかなり元の関数のパラメータと近い

フィッティング結果になったと思う。フィッティングするには十分なデータを用いてフィッティングするのが良い。

では点数を減らさないように移動平均するにはどうすればいいのか。

答えは単純で、データ点数を間引かないで移動平均することが重要である。

では移動平均した際にデメリットは発生しないのか？以下の例を見てみよう。

５．移動平均が１００の場合



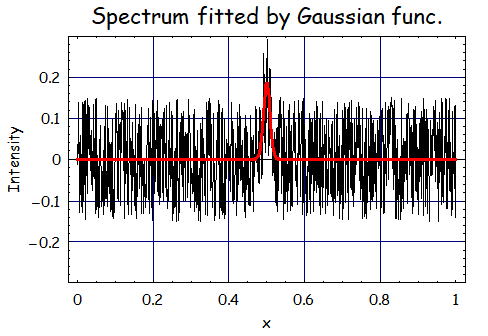
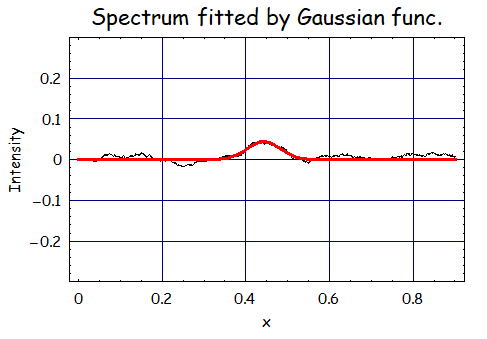
今回はランダムノイズをΔｙ＝±0.15加えて、A＝0.15、ｍ＝0.5、σ＝0.01のような鋭いピークの場合、

移動平均するとどのような結果になるのか見てみよう。左のグラフは移動平均なしの場合である。

フィッティングの結果は、A＝0.19、ｍ＝0.5、σ＝0.0088である。

かなり結果としては元のデータに近い値になっている。

一方で移動平均した場合、フィッティングの結果は、A＝0.044、ｍ＝0.44、σ＝0.039である。

ノイズはかなり低減されている為ピークも見やすくなっているが、信号自体がブロードになっている。

このように移動平均を行うことで信号がブロードになるため信号の形状を解析する際には非常に注意が必要となる。

つまり本来のピークとは異なる為注意が必要ということである。

移動平均ノイズを減らしながらピークの最大値を減らさない平滑化方法はないのか次節考えてみよう