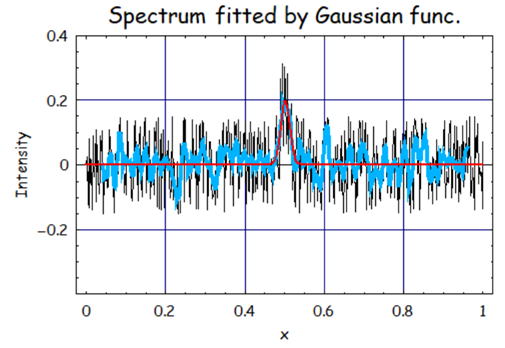
先ほど信号をGaussian Filterで重み付けを行ったが、分析化学でよく使われている
Saviztky Golay法に関して議論する。1964年両者が発表したデータのスムージング手法である。
この手法は、隣接する2N+1のデータに対して、m次の多項式で近似して2N+1の中央値の元データを
そのxの位置の近似多項式のy(x)に置き換えていくことで、ノイズを低減させていきます。
この手法は実質的に重み付き移動平均である。
特徴
- 多項式近似にもかかわらず、近似に使うデータの点数と近似する多項式の次数だけで係数が決まる
- スムージングだけでなく、平滑化微分も計算できる
(3次以上の多項式で近似する場合は2次微分以上も可能) - スムージングの手法にもかかわらず、ピークが鈍りにくい
- 実質は重み付き移動平均なので、処理が高速
このようにこのフィルタは上記の特徴を持つために分析科学でよく用いられている。
Saviztky Golayの導出
まず、最初に等間隔で並んだデータについて、2N+1点をm次多項式
で近似することを考えます。
この時データのxの値は−NΔx 〜 NΔxと書くことができます。
するとxとyのデータの組は、(−NΔx、y(−NΔx))、(−(N-1)Δx、y(−(N-1)Δx))、、、、
(NΔx、y(NΔx))となる。これらのウィンドウ内にあるデータ点をm次の多項式で近似フィットする
と考えればよくその時の最小二乗法は、
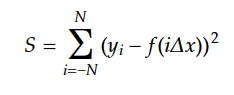
であり、これを偏微分して0と置いた時の解は、
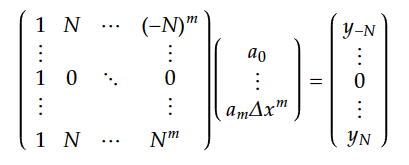
を解くことなる。左の行列式をXと置くと、近似多項式の係数(a0、、、、amΔxm)は、
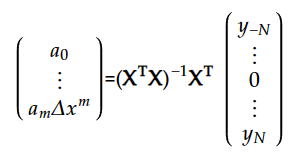
で与えられます。
Savitzky Golay法は実際の処理で近似多項式に置き換えられるのは2N+1の中央の点のみで
他の値は使わない。その時の値はf(x)=f(0)の時の値である。つまり、これはf(0)=a0と同じになる。
このa0は元データy(NΔx)に依存していないので、行列の1行目とyデータ列の内積を計算するだけで
求めることができる。しかもyとの行列積をとる行列はデータ数Nとm次に依存するだけで、
データyに依存しないので毎回行列要素は同じであるので、一回事前に計算しておけば
使いまわすことができる。つまり各点yの近似を求める際に毎回計算する必要がない。
また微分データもf’(0)=a1Δx、f”(0)=2 x a2Δx^2であるので微分データも簡単に求めることができます。
では実際にSavitzkyGolay法を用いて平滑化する様子を見てみよう。
前回と同様に元信号は、A=0.2、m=0.5、σ=0.01のガウス信号に、
ノイズ信号±0.15を持つランダムノイズを加えた信号である。
1.フィッティング多項式次数:m=5、Windowサイズ(フィッティングデータ点数)=9、微分次数=0の時
SavitzkyGolay係数、{0.034965, -0.128205, 0.0699301, 0.314685, 0.417249,
0.314685, 0.0699301, -0.128205, 0.034965}はフィッティングされるデータ点数と同じ要素数をもつ。
この係数とウィンドウサイズ内にある各9データとの内積をとることで、1番目のデータを生成する。
上でも述べたがこの係数は、m、Windowサイズ、微分次数が決まれば一意に決まる。
実際にSavitzkyGolay法で平滑化した結果を示す。
フィッティング結果はA=0.22、m=0.500、σ=0.011である。若干のノイズ成分は小さくなっているが、
まだ元データに近しい信号であるもののフィッティング結果元のガウス関数に近くよくフィッティングできている。
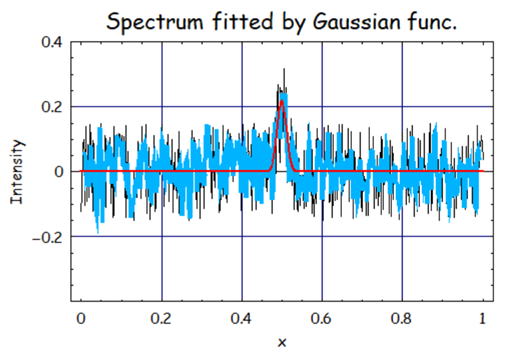
2.フィッティング多項式次数:m=5、Windowサイズ(フィッティングデータ点数)=40、微分次数=0の時
では次にWindowサイズだけを大きくしてみよう。フィッティングデータ点数を増やしているので
データはより平滑化されることが予想される。
見てわかるように高周波成分はほとんどきれいに除外できていることがわかる。
一方でWindowサイズより大きい周波数成分Δx:0.002xWindowサイズ:40=0.08以上のノイズは
残っている。一方で今回のガウス信号は上記0.08よりは細い信号であるのにもかかわらず、
信号ははっきりと見て取れる。
この平滑化した信号のフィッティング結果は、A=0.14、m=0.496、σ=0.012である。
信号の強度は弱くなっているものの信号はしっかりとわかる。
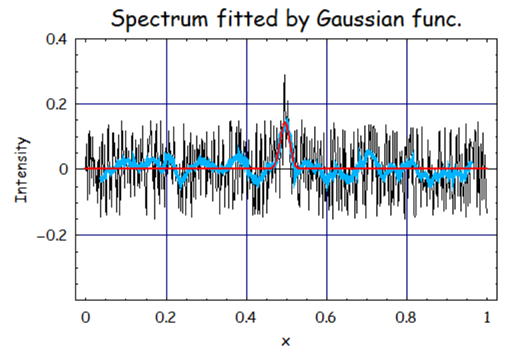
3.フィッティング多項式次数:m=10、Windowサイズ(フィッティングデータ点数)=40、微分次数=0の時
では次にフィッティング次数を増やして見よう、フィッティング次数が増えるとより高周波まで近似できるので、
ノイズは消しづらいが、信号強度は維持されるということが予想される。
平滑化した信号のフィッティング結果は、A=0.196、m=0.501、σ=0.012である。
データ信号は復活して0.2に近づいているが、ノイズの量は増加している。
結局計算負荷も考えるとウィンドウサイズを変えてある程度ほしいSN比まで来たら、
そこまで次数をあげても結局Sは増えるがSNは悪化するので、mを積極的にあげる理由は内容に思われる。
本格的に複雑な信号の形をしていた場合は次数をあげる必要があるのかもしれないが、
今回はそこまで議論できていない。