

先ほどSavitzky Golay法を用いてSmoothingやその微分を行ってピーク検出を行った。
次にSavitzky Golay法ほど有名ではないが1922年にWhittakerによって発表されたSmoothing法である。
この後、2003年にEilersが2003年の論文にWhittakerの方式を応用したAsLS法というベースライン推定法を
発表すると分光スペクトルやクロマトグラムのベースライン推定手法としてWhittakerに注目が集まり、
数々の応用手法が作られた。WhittakerのSmoothing法の特徴として
特徴
- 比較的短いコードで実現できる
- 疎行列の計算に対応していれば、多数の観測値に対しても比較的短時間でスムージングできる
- 欠落データに対応できる
- 滑らかさを制御できる
Whittakerの導出
まず、観測された測定データの列を y=(y1、y2、・・・・、ym)とする。
この値に通常ノイズなどが乗っていることからデータをグラフに描くとなめらかな線になりません。
次に滑らかなデータ列 z=(z1、z2、・・・・、zm)を考え、zをyに適合させることを考える。
そのためには、2つのことを考慮に入れる必要があります。
- yに対するzへの適合具合 → 差の二乗和 (yn−zn)^2
- zの粗さ → zのs回差分の二乗和 (Δs zn)^2
であリ、それぞれを数式で表現することができる。
zがなめらがであるほど、ノイズがあるデータ列yから乖離するため、両者は相反する要素となる。
以上から、両者を考慮した内容を数式に落とし込むとペナルティ付き最小二乗法の問題となる。
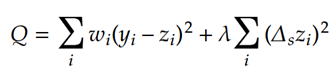
ここでwiは重みを表し、0≦wi≦1です。欠落データや外れ値などに対して、0または0に近い値を
与えます。また、λはペナルティ係数です。λを大きくすれば粗さの項が優勢となり、より滑らかな
曲線生成することができます。
上記の数式を行列とベクトルで表すと、
となります。
ここで、Wは重みw=(w1、w2、・・・、wm)を対角に配置した対角行列、Dsは、
となるような行列です。例えば、m=3、s=1では、
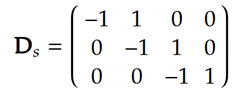
m=5、s=3であれば、
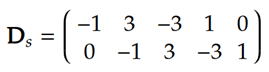
となる。
次に上にある行列式をzで偏微分して、
それを0と滑らかな関数zで評価関数Qの変化が最小となる場合を計算すると
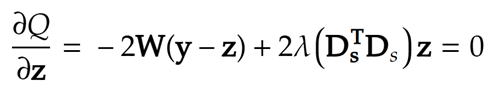
となり、
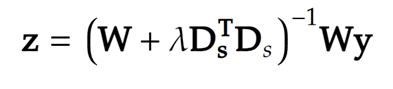
である。これを計算することで、滑らかなデータ列zを求めることができます。
Eilersによるとs=2にすることでうまく機能することが多いとのことです。
では実際にWhittaker Smoothingを用いて平滑化する様子を見てみよう。
前回と同様に元信号は、A=0.2、m=0.5、σ=0.01のガウス信号に、
ノイズ信号±0.15を持つランダムノイズを加えた元信号を考える。
1.S=2、λ=1、Wi=1の場合
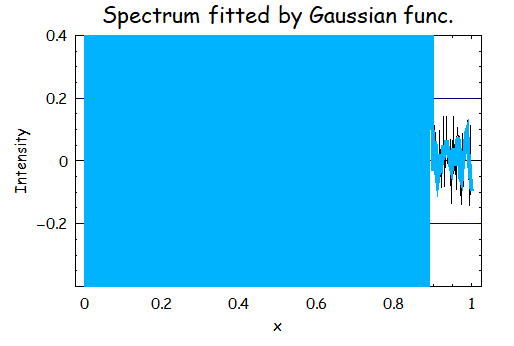
この結果を見てみると、完全に0.9より小さいところで発散している。
ここでλを大きくするか、重みWiを小さくするかしないとこの発散は止められない。
2.S=2、λ=10^5、Wi=1の場合
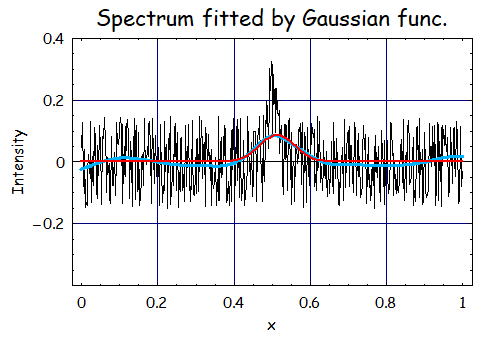
次にλを大きくした際にどのような結果になるのかを検討した。
発散は抑えられているし、ノイズは非常によく平滑化されている。その為か、信号がブロードになっており
この時のフィッティング結果はA=0.086、m=0.513、σ=0.047である。
この結果を見ても、振幅がつぶれているのがわかる。
3.S=2、λ=1、Wi=0.5の場合
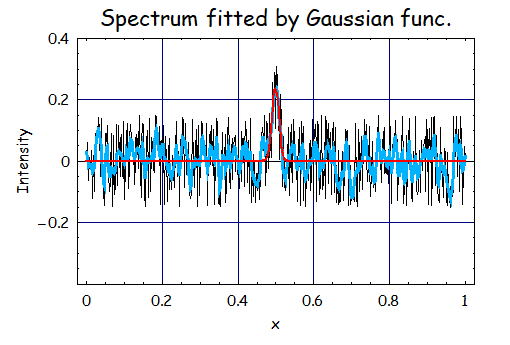
重みWiを0.5に変えてみた際にどのような結果になるのかを検討した。
重みWiを小さくすることで収束しているのが分かる。信号も維持的でいるが、ノイズの高周波成分が取り切れていない為、
先ほどのλを変更する場合と比較して平滑化、特に高周波成分の平滑化、はあまりできていない。
この時のフィッティング結果はA=0.24、m=0.499、σ=0.0092である。
フィッティングはよくできているが、実際は複数回フィッティング処理を行うと、
ノイズをフィッティングしてしまうことも起こってしまう。その為もう少し高周波を抑制したい。
4.S=2、λ=10、Wi=0.5の場合
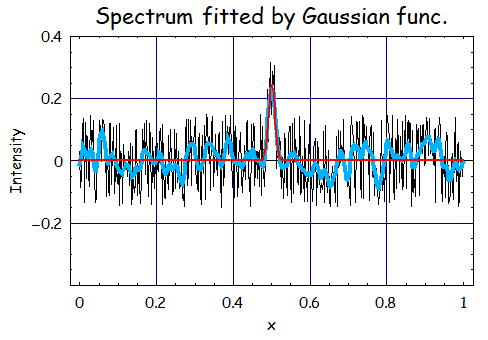
先ほどの検討から
重みλを変更すると、低・高周波両方ともノイズを低減することが可能であるが、真の信号もブロードにする
一方、
Wiを変更すると、低周波のノイズは低減でき、信号もブロードにならないが、高周波のノイズは残ってしまう。
ここら辺のバランスを整えることが必要になるので、
重みWiを0.5に変えて、λを10にした結果を上に示す。今回も収束して、平滑化もなされている。
ノイズの高周波成分は緩やかになっている一方で、ピーク強度もそこまで弱くなっていない。
この時のフィッティング結果はA=0.243、m=0.500、σ=0.0087である。
