
(1)SS-OCT方式のメリット/デメリット
前節でみてきたとおり、SS-OCTのメリットが大きいということが次の点にあることが分かった
| TD-OCTと比べて | SD-OCTと比べて | |
|---|---|---|
| メリット | ・感度が100倍以上高い | ・ディテクタを選ばない ・高速化が可能である ・動きに強い |
| デメリット | ・装置の性能が光源特性に強く依存する | ・装置の性能が光源特性に強く依存する |
これからわかるように、SS-OCTが現状のよい光源さえつくることができたら、他方式と比べて性能が良く測定対象物への汎用性があることが分かる。
よって、この節ではSS-OCTの基本原理に関してまずは説明していこうと思う。
(2)SS-OCT方式の基本原理
SS-OCTの全体の構成は以下の通りであった
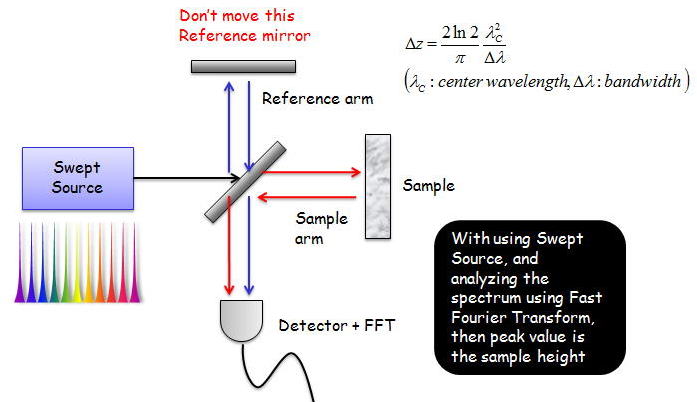
構成要素は大きく分けて、①波長走査型光源、②干渉計と③検出器(PD or APD)+FFT計算機 からなる
SS-OCTの分解能と測定距離(測定レンジ)はどのように記述できるのだろうか?
基本原理
SS-OCTの基本原理について説明する。
上記のような干渉計の場合、ディテクタで検出される干渉信号は、
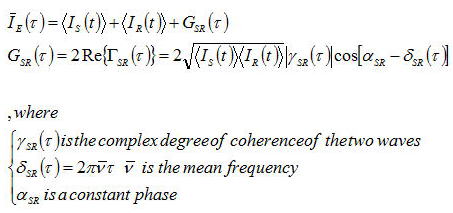
となる。ここで、干渉項Gはもしサンプル、ミラーやビームススプリッターがなく光源のみであった場合に単純化すると、
と当たり前であるが、光源のみの項としてあらわされる。
さらに、サンプルによる入射電場への影響は伝達関数h(t)を用いて
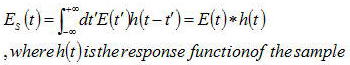
とあらわせる。
上記の二つの式から、干渉項Gが光源のみであったのに加えて、このサンプルからの影響を取り入れることで、
干渉項Gは以下の式で表せる。
伝達関数h(τ)の考え方としては、いくつかのモデルが提唱されているが、簡単でよく表せるモデルとしては
各界面層からのフレネル反射を考えるモデルがある。
z分解能
OCTのz方向への分解能はどのように表現できるであろうか?この疑問に関して説明する。
干渉項Gをフーリエ変換する。
となる。これも当然であるがフーリエ空間上で光源の周波数帯域以上は干渉項は出現しないことを上式は意味する。
このことが、分解能に制限を与える。(物質側の応答関数 or 伝達関数は様々な周波数に応答可能であるとする)
よって、光源のみからの制限から、光源の周波数帯域は通常ガウス関数である程度近似できる。
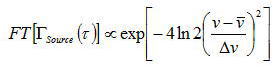
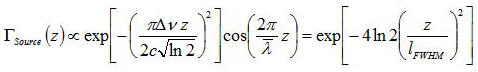
上式は光源のスペクトルをzに関して逆フーリエ変換したときに得られる結果である。
上式からz方向の分解能は、干渉が往復であることを考慮して
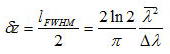
となる。ではSLDを利用した際にどの程度の分解能が得られるのか計算してみよう。
通常700-900nm帯域と1300-1500nm帯域があるが前者で考えよう。
800nmでは現在ではよくても50nm程度の波長帯域の製品がある。この値をもとに計算してみると、5.65um程度になることが分かる
測定レンジ
測定レンジはサンプリング定理によって決まっており、
Nは画像のサンプリング枚数で、δzはz分解能である。
通常理想的な光源(完全な輝線スペクトルなら)Nはいくらでも大きくとれば、測定レンジもいくらでも大きくなるわけであるが、
実際は光源が輝線でないため、最終的にはそちらの方で測定レンジの制約を受ける
