Raman散乱の古典論では、
- 入射光を平面電磁場
- 分子を分極率を持つ粒子としてモデル化
この場合、散乱光は入射電場により、分子に誘起された誘起双極子から球面電磁場を放出する。
入射電磁場ベクトルをEiとすると、
eiは偏光ベクトル、ωiは角振動数である。
この時ラマン散乱の機構は以下の図のように表される。
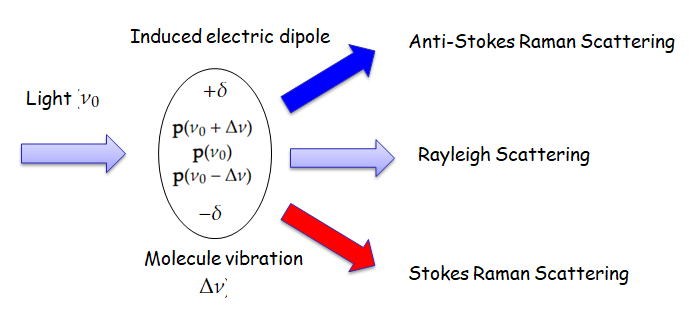
図に示すように、入射光と分子振動の相互作用により振動数が異なる3種類の電気双極子（ν、ν-Δν、ν+Δν）が誘起され、
それぞれ、レイリー散乱、ストークスラマン散乱、アンチストークスラマン散乱の光が放出される。
（A）誘起電気双極子
もう少し数式を用いて誘起電気双極子能率（モーメント）表現すると、
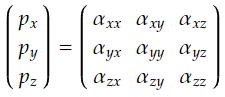
で表される。αは分極率テンソルで、αは電場中の分子に誘起される電気双極子能率の方向と大きさを表す量で、
分子内の電子分布とその動きやすさを表す量です。よって、この誘起された電気双極子は入射電場により振動することを表す。
次に、入射電場とこの誘起電気双極子との相互作用を考えるにあたり、基準座標系Qk を用いる。
分子内の核配置は平衡位置とその周りの変位座標で表すことができる。
この変位座標を分子の点群の規約表現に属する1組の座標が基準座標である。
αを平衡位置の周りで基準座標Qkのベキ級数として展開して、第一項まで残すと、
は原子核の平衡位置における分極率、
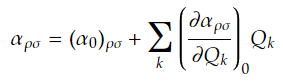
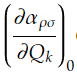は核の平衡位置における分極率成分
のk番目の基準座標による微係数である。さらに、入射電場あるなしに関わらず、分子は基準座標に沿って周期的に運動しているため、
Qkは振幅Qk0と基準角振動数ωk (上の図のΔνk\\に相当)で以下で表される。
この分子の運動を上の分極率テンソルαのべき級数展開の式に代入すると、
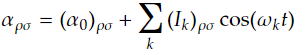
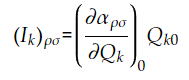
Ikは周期的に変動する部分の振幅である。
分極率テンソルαが定式化出来たので、これを先ほどの誘起電気双極子の式に代入すると、
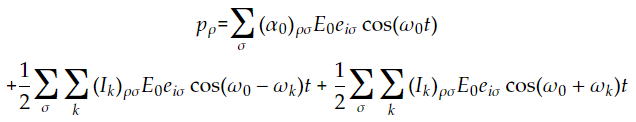
という式が導出される。これは、3つの各周波数を持った誘起電気双極子があることを意味しており、
したがって、それらの3つの角振動数を持った電磁波を放出する。
これら3つの電磁波は、レイリー散乱、ストークスラマン散乱、アンチストークスラマン散乱となる。
（B）誘起電気双極子から放出される電場
では、誘起電気双極子能率(モーメント)から放出される電場はどのように記述できるだろうか？
分子を原点に置き、放出される球面散乱波の位置Rにおける電場ベクトルを振幅Es、偏光ベクトルesの積として表す。
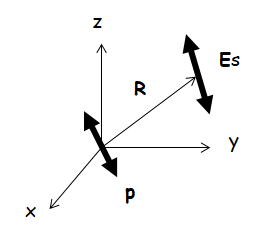
マクスウェル方程式(双極子が振動してるとどのような電磁場が出るのか計算できる)により、Esはpと次のように関係付けられる。
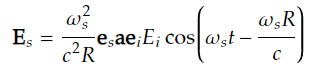
ここでωsは散乱光の角振動数、cは光速度である。
これを２乗することで、入射平面電場Iiと、散乱球面電磁波の強度IsR^2が関係づけられて
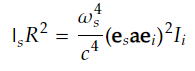
これが光散乱の強度とその角度依存性を表す古典論での式になる。
ここで、aは上記で表した散乱テンソルで、レイリー散乱の場合a=I0、ラマン散乱の場合はa=Ik/2である。
（C）誘起電気双極子の放出電場から分かること
- ストークスラマン散乱とアンチストークスラマン散乱は古典論の枠組みでは共通
- 散乱光強度は、入射強度に比例する(線形光学過程)
- 散乱光強度は、散乱テンソルの二乗に比例する
- 散乱光強度は、角振動数ωsの４乗に比例する
よく、実験においてどの波長を用いるとラマン散乱強度が強く得られるか？という疑問が出てくる。
ここではラマン散乱観測に使われる代表的な高出力可能なレーザ波長(460, 532, 633, 780)に対して、
780nmを基準１にしたときに波長の4乗則がどう効くのか比較してみよう。
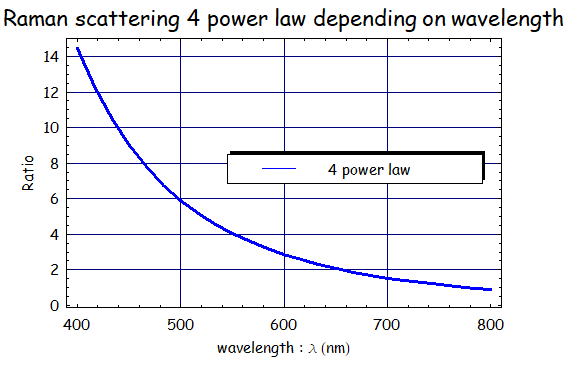
短波長化することでラマン散乱強度が増強することが見て取れる。
しかし、単純に短波超過すれば良いわけではなく
他の光学系の感度（センサー）やコストの影響も考える必要がある。
