Raman散乱の古典論で述べたように、以下の微分分極率テンソルのいずれかの成分が
ゼロでないことが必要である。
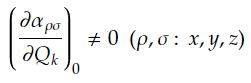
調和振動近似の場合に、ラマンスペクトルの選択律は以下のようになる。
ラマンスペクトルの選択律
ラマンスペクトルには、分極率の変化が生じるような基準振動の基本音が観測される。
分極率は分子の体積(電子雲の体積)に相当するから、基準振動により体積が変化するような振動が
ラマンスペクトルに観測されると考えてもよい。
さらに有用な通則を与えておくと、
- 対称心を持つ分子では、
- ラマン活性な振動は、対照心に対する反転操作に対して対称な振動である
- 赤外活性な振動は、その操作に対して反対称な振動である。
- 赤外とラマン両方に不活性なことがあるが、両方に活性になることはない。このことを、交互禁制律と呼ぶ。
- 振動スペクトルを解析するには、赤外とラマン両方のスペクトルを解析するのが望ましい。
- 全対称振動は必ずラマン活性である。(群論の全対称表現には、x^2,y^2,z^2が属している為。)
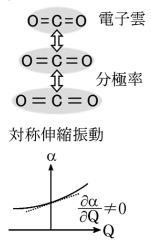
では、直線三原子分子であるCO2分子の基準振動に伴う分極率の変化を図に模式的に示した。
図では電子雲が持つ電荷分布の相対的な偏りは分子の分極率(α)を表している。
この分子には3つの振動が考えられ、ぞれぞれの振動モードの下に振幅(Q)とαとの関係を示している。
- 2つのC=O結合が対称に振動する対称伸縮振動ν1
よって、一次微分がゼロでないためにラマン活性である
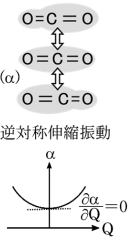
- 2つのC=O結合が反対称に振動する反対称伸縮振動ν2
その為、分子の電子雲で見た時の分極率の変化は一旦減少して平衡状態になり増加していく。
故に、一次微分はゼロとなり、ラマン不活性となる。
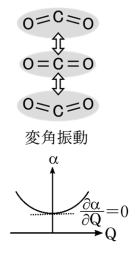
- 2つのC=O結合のなす角が変わる変角振動ν3
最後にこの場合だが、炭素原子を中心に2つの酸素原子が上下に同期しながら動いているが、
平衡位置に対して前後で分極率が減少して増加する。
つまり、分極率の変化はあるが、一次微分はゼロになる。故に、ラマン不活性となる。
上の図は以下を参照させて頂いた。
p504.pdf (jsac.jp)
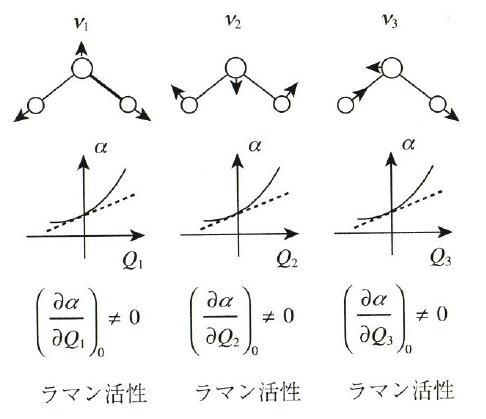
次に、水分子に関して考えると、そもそもの分子構造が非対称であるので、どの振動モードも分極率の変化は
ゼロでないのでラマン活性となる。