
幾何光学の基本的な考えは光線追跡である。光線追跡で光が曲がるのは次の二つの場合のみである。
①屈折率の異なる媒質を通過するとき
②反射率のある媒質に入射したとき
の二つであり、それ以外は直進する。
この節から当分の間、薄肉レンズ(レンズの厚みを考えない;Thin lens)と
近軸光線(光線が光軸に対して浅い角度;paraxial ray)の場合を仮定して議論していく。
レンズの公式
まずここでは、①の屈折率のある媒質に関してレンズを例に説明する
物体側(object)から発散された光はレンズを通過すると像側(image)の一点で集光する。
その様子を表した図が下で表してある。
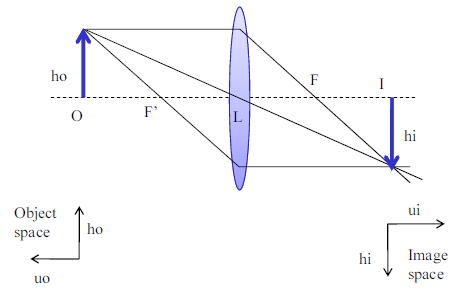
ここでよくレンズの公式として以下のものがよく記載されているがこれはどのような時に成立するのだろうか
という点を考えると
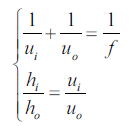
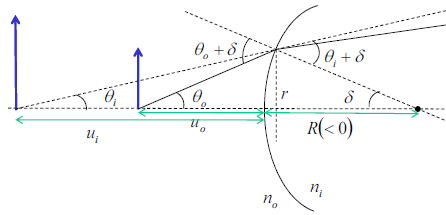
レンズの片側で曲率Rが負の場合を考える
これの三角形の部分と屈折の公式を合わせて(今回は近軸近似が成り立つ範囲で式を立てる)
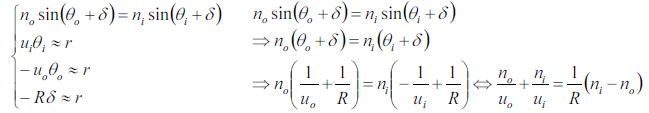
さらに、レンズの右側(R2>0)で曲率が正の場合を考えると、
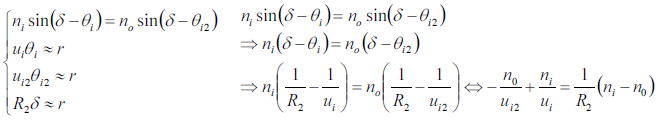
である上式二つを整理すると
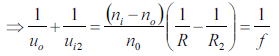
となりレンズの公式が導かれる。(添え字は修正してください)
