扨怓廂嵎
憸柺榩嬋
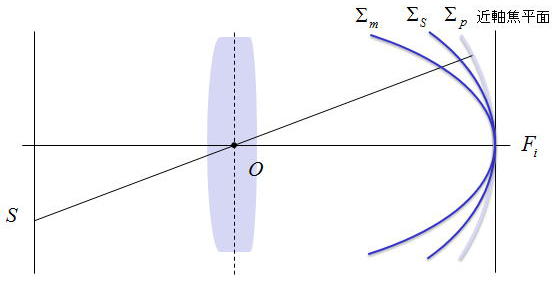
岝幉偵悅捈側暯柺暔懱偼嬤幉椞堟偺傒傎傏暯柺偲偟偰寢憸偝傟傞丅峀偑傝偺偁傞奐岥偱摼傜傟傞榩嬋偟偨柍廂嵎憸柺偼丄
儁僢僣僶乕儖偺憸柺榩嬋乮Petzval field curvature乯偲偟偰抦傜傟傞堦偮偺庡梫廂嵎偱偁傞丅
嬶懱揑偵偦偺條巕傪尒偰傒傛偆丅
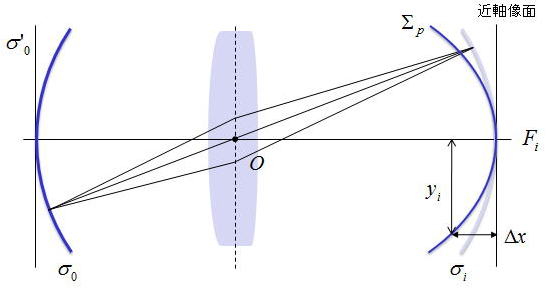
媴柺暔懱偺堦晹冃o偑丄儗儞僘偵傛偭偰傗偼傝媴柺偺堦晹冃i偲偟偰寢憸偟偰偄傞丅冃o偲冃i偺拞怱偼O偱偁傞丅
冃o傪冃o'偵暯扲壔偡傞偲丄奺憸揰偼偦傟偧傟偺庡梫岝慄偵増偭偰儗儞僘偺傎偆偵堏摦偟丄
曻暔柺偱偁傞儁僢僣僶乕儖柺乮Petzval surface乯儼p偑宍惉偝傟傞丅惓儗儞僘偺応崌丄儁僢僣僶乕儖柺偼暔懱柺偵懳偟偰嬤偯偔傛偆偵
嬋偑偭偰偄偔偑丄晧偺儗儞僘偱偼暔懱柺偐傜墦偞偐傞傛偆偵奜岦偒偵嬋偑偭偰偄傞丅
偟偨偑偭偰丄惓偲晧偺儗儞僘傪慻傒崌傢偣傞偲憸柺榩嬋傪懪偪徚偣傞偙偲偑柧傜偐偱偁傞丅
崅偝yi偺儁僢僣僶乕儖柺忋偺憸揰偺丄嬤幉憸偺暯柺偐傜偺曄埵検嚈倶偼丄
岝妛宯傪峔惉偡傞倣枃偺儗儞僘偺孅愜棪偲徟揰嫍棧傪nj偲fj偲偟偰丄
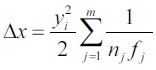
偱梌偊傜傟偰偄傞丅忋婰偺幃偐傜儗儞僘偺埵抲傗宍忬偁傞偄偼峣傝偺埵抲偑曄傢偭偰傕丄儁僢僣僶乕儖柺偼晄曄偱偁傞丅
偙偺偲偒柧傜偐側傛偆偵嚈倶亖侽偵側傞傛偆偵偡傞偲丄憸柺榩嬋偑側偄傛偆偵偡傞偙偲偑偱偒傞丅
旕揰廂嵎偲憸柺榩嬋偺娭學
旕揰廂嵎偲憸柺榩嬋偼枾愙偵娭學偟偰偄傞丅儊儕僆僕僫儖暯柺儼m偲僒僕僞儖暯柺儼s偱偺擇偮偺曻暔柺忬偺憸柺偑偁傞丅
戞侾偍傛傃戞俀偺憸揰慡懱偑宍惉偝傟傞儼m偲儼s偵偍偄偰丄儼m忋偺擟堄偺崅偝yi偲懳墳偡傞儼s忋偺懳墳揰偼丄儁僢僣僶乕儖柺偵
娭偟偰摨偠懁偵偁傞偑丄儼m忋偺揰偺傎偆偑儼s傛傝儼p偐傜俁攞墦偔棧傟偰偄傞丅
旕揰廂嵎偑側偗傟偽儼倱偲儼m偼儼p偵廳側傞丅