---

色収差

薄肉色消しダブレット

色収差に関して述べてきたが、ここではその色収差を抑える方法を提示する

正と負で色の出方が逆なので、正負二枚の薄肉レンズを組み合わせれば、少なくとも赤と青はきっちりと重ねることができる。

このような配置を特定の２波長に関して色消しされているという。

ｄだけ離れた２枚のレンズでは、薄肉のレンズの公式より、



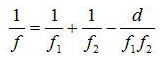
で上式を以下の式をもちいて変形すると





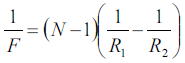
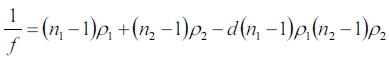
となる。

焦点距離ｆは波長によって異なるため、色消しをするためには、




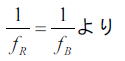
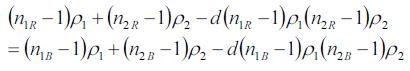
が得られる。

上式の条件を満たすような曲率ρや面間距離ｄを選択することで下の図に示したように、

ある波長（ここでは青と赤）に対して色消しをすることが可能である。



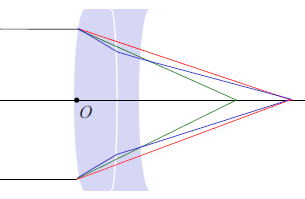
特に重要なケースは、d=0のとき、つまり２枚のレンズが接触している場合である。

なぜ、接触しているレンズが重要なのかというと、詳しい説明はしないが、色収差以外に球面収差を凸レンズと凹レンズを組み合わせて

凹レンズの屈折率を高くすると、凸レンズの球面収差が凹レンズで打ち消せることにある。

話をもとに戻して、２枚のレンズを接触させると、上式でd=0なので、



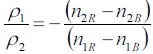
である。さらに、焦点距離と曲率と屈折率の関係から、



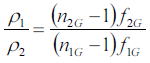
である。２式を整理すると、



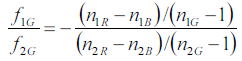
であり、



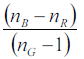
の形が分母分子で共通項となっている。この項を２種類のレンズ材の分散能（dispersive power）として知られており、

その逆数は分散率（dispersive index）、Vナンバーあるいはアッべ数（Abbe number）などと呼ばれている。

アッべ数は正である。その理由はNは常に１より大きいので上式の分母は正である。さらに赤と青の屈折率は

必ず青のほうが屈折率が高いので分子も正の値になる。よってアッべ数は正となり、このことが次の重要な帰結を導く。

２つ上の式で左辺は焦点距離の比がアッべ数の比の符号を反転した形だが、赤と青の色収差をとるとき、

どちらかのｆが正ならもう一方は負に必ずなることを意味している。