---

Prism（プリズム）光学

プリズムは昔からニュートンが光がさまざまな波長を含む色であることを理解するのに使われるなど、

古くから使われている光学部品の一つである。

ここでは、そのプリズムの波長分散性（つまり、波長を分解する性質）に関して順を追って考察してみようと思う。

プリズムに入射する方向に対してどの程度進路を変更するのかは角度δで与えられる。

これをプリズムによるフレ角（angle of deviation）と呼ぶ。

プリズムの頂角をαとすると、図から



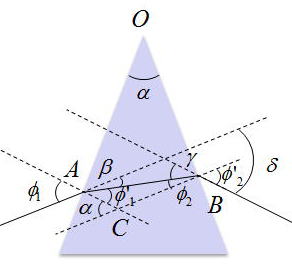
β、γ、δはそれぞれ

　　　　　　　

と記述することができる。

ここで、三角形OACと三角形OBCはそれぞれ直角三角形なので四角形OABCは円に内接する。（高校数学だよ）

よってCの角度はαとなる（中学数学だよ）。以上と、



の関係からフレ角δは



となる。

Prism（プリズム）最小のフレ角と屈折率計測

次に、プリズムの最小のフレ角はどのような入射角度で入れることで、どの程度の値をとるのかに関して考察する

スネルの法則と上式のδの関係式を用いて、フレ角が最小になる時、δの微分量が０となるので、



よって、頂角の半分の角度で入射させたとき、フレ角が最小になり、光線が対称の軌跡を描く。

下のグラフは入射角度をふったさいのフレ角がどのように変化するのかを計算した結果である。




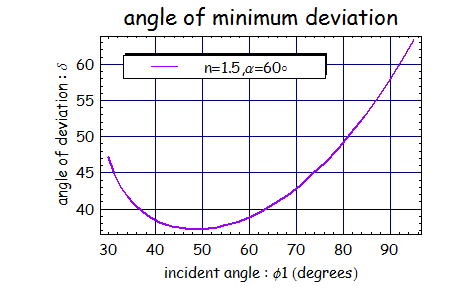
ところでこの最小のフレ角を用いてプリズムの屈折率を計測するとことが可能である。

屈折率とフレ角の関係は、δが最小のとき



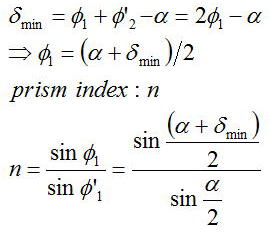
という関係がある。つまり、最小のフレ角と頂角がわかれば、プリズムの屈折率を計算できる。

頂角の計測は分度器か何かで測ればよいとして、

フレ角に関してはプリズム分光器を用いる。プリズムを回転させることでプリズムへの入射光が変化していく。

フレ角δが最小をとるということは結像側へのスリット像の動きが反転する瞬間がある。

その時が最小のフレ角になっている配置であり、その角度を測ることでフレ角の最小値の量が分かる