---

ニュートン形式のレンズの公式


ここではニュートン形式のレンズの公式に関して説明する




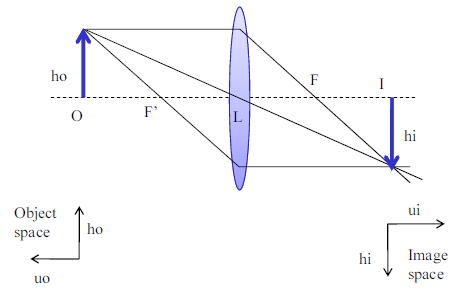
三角形の相似を考えると以下の関係が得られる



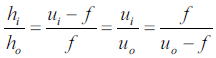
第二式と第三式から前節で述べたレンズの公式（こちらはよくガウスのレンズの公式と呼ぶ）



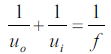
が導かれるが、ニュートンは、



というニュートン形式のレンズの公式を導いた

この式は1704年に出版されたニュートンの光学「Opticks」ではじめて述べられた。

この式は物体uiがｆよりもレンズから左にｆより遠い位置にあるとき、像uoは必ずレンズの右側にあることを述べている
（ui-fが正でf^2も必ず正の値を持つため）


横倍率

ここで次の横倍率の定義する。

横倍率とは光軸と垂直方向の物体と像の長さの比であるので、



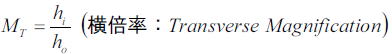
単レンズの実像ではuiもuoも正の値になるため、一番上の式からMTは正となる。

そのため1枚の単レンズで形成された像は、すべて倒立している。


縦倍率

　次に縦倍率の定義する。

縦倍率とは物体と像の軸方向の微小長さの比である。





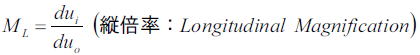
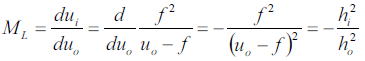
となるこの式は縦倍率は横倍率の二乗に符号を反転させた値となる

上式の符号が逆であることから
軸方向でレンズに向かう物体の形状の像はレンズから離れる方向になることを示唆している。
つまり、物体が右向きの矢印ならば、その像は右向きの矢印となり向きが変わらないことを意味する