---

厚肉レンズ


厚肉レンズとは、下図に示したように、レンズの厚みがもはや無視できないレンズを示している。

あるいは、もっと一般的に言うならば、厚肉レンズは単に１枚レンズではなく、いくつかの単レンズからなる光学系とも考えることができる。




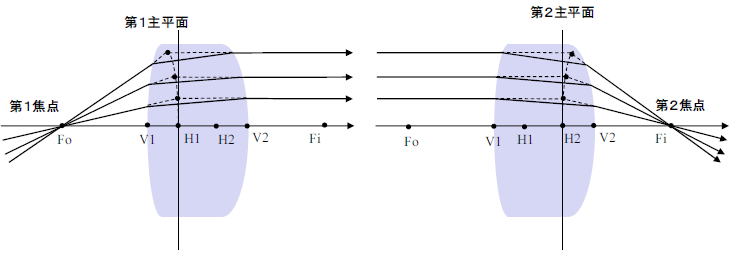
図では、第１および第２焦点、あるいは物焦点と像焦点FoとFiは、二つのもっとも外側にあるレンズ面からの距離である。

この場合それぞれおなじみの前側焦点距離と後側焦点距離となる。

入射光線と出射光線は延長するとある一点で交わり、この点が各高さでの入射光線で形成される点群はレンズの内側か外側で曲面を形成する。

この曲面は、近軸領域では平面とみなすことができ、主平面（principal plane）と名付けられており、主平面と光軸とが交わる点を第１主点H1と第２主点H2として知られている。

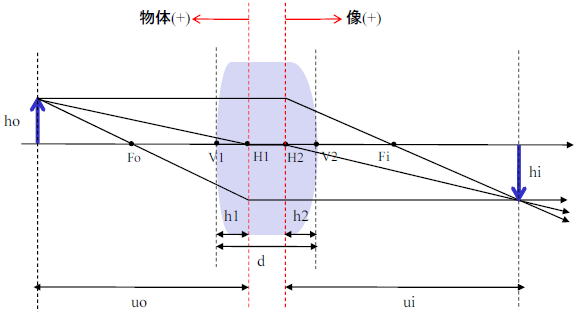
ここで、厚肉レンズの結像を考える上で符号をもう一度きちんと定義しよう。

物体と像側の距離はそれぞれ第１主平面と第２主平面を基準として測る。（符号に関しては各種定義があるので、書籍ごとに注意されたい）

また、距離や長さに関係した量が上下方向の量であるときには、下から上に向かって測る場合は正、逆は負であるとする。

曲率は薄肉とは今回異なり、中心がレンズ端より左なら負、中心がレンズ端より右なら正であるとすることに注意。（もし嫌なら符号を取り直してほしい。）

主平面に関しては正ならばレンズの内側（媒質側）、負ならばレンズの外側（空気側）になることにも注意されたい

ここでは、いくつか数式や符号が出てくるがそれらが重要ではない。実際でのレンズ系での光線は、光線追跡と呼ばれる次節でのやり方で結像を考える（光線を追跡するやり方。ここでは、薄肉レンズと厚肉レンズがどこが異なり、どこが同じなのかをきちんと理解していただければよいかと思う。式を覚えたり使いこなせる必要はない。）

では、厚肉レンズでの結像に関して考えてみる。



ここでは、導出までは行わないが、たくさんの代数操作を経てると、面白い結果が得られる。それは二つの主平面からの共役な２点に関してガウスの式が成立し、



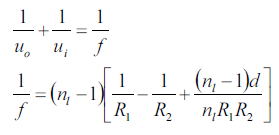
が得られる。（焦点距離の定義がレンズの厚みを考慮した項が追加されている点が異なる。もちろんｄ→０にすれば薄肉レンズのときに議論したレンズの公式であることがいえる）

で、やはり気になるのが光線追跡を行う際に主平面がどこにできるかを知っておく必要がある。

つまり、物体はレンズの中心から、もしくは、レンズの端からいくつの位置に置いたときという形でしかわからないため、ガウスのレンズ公式を用いて像位置を計算するときには主平面の位置が分からないuo、uiを計算できないからである。

結果だけ述べると、主平面の位置は、



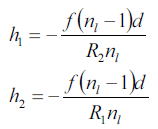
である。

ここで、一つ確認しておく必要がある事柄がある。

それは主平面と光軸が交わった二つの主点はお互いどのような関係にあるのだろうかという点である

ガウスのレンズの公式から考えると、uo=0ならばｆが有限値であるためにui=0である必要がある。

つまり、H1はH2に結像することになる。また倍率に関しては、１となる。

このことは以下の重要な帰結を与える。

第一主平面上のある点に向かって入射する光線はあたかも第二主平面上の同じ高さからある角度で出射する。

つまり、光線があたかも主平面間を短縮すれば薄肉の場合と同じように扱えることを示唆している。
（注意としては薄肉は主平面間距離が０であるが、厚肉は主平面間距離は有限であること）