---

Matrix法（マトリックス法）


厚肉レンズを扱う際に主平面（倍率１となる共役点：共役とは物体と像のこと）を意識して、薄肉レンズと同様に扱うこと。

と偉そうに記載したが、実際のレンズの設計においては光線追跡という別のやり方で何本か入射光線を入れて、

それら光線のレンズ系での軌跡を追うことで像面での像特性を評価することを行っている。

最近ではPCのスペックが向上したことから、２次元に光線を入射させて、すべての光線をもとに評価することがなされている。

かつては人が手計算でやるなら一本の光線追跡で10-15分と時間がかかってしまっていた。


符号

何度も出てきて恐縮なのだが、ここでマトリックス法における（というか、この節で扱う）符号に関してもう一度定義しておく

何度もやることでその都度符号の定義は必ず確認してもらう習慣をつけてもらいたい

ここでは光は左から右へ進むので、

・左から右を正の向き
・下から上を正の向き

と定義する（物体と像側で座標系をここでは作らない）

ここでは始点を○で終点を→で書くことにする。また媒質が変わる境界面を始点とすることを約束事にする。




光線追跡で用いられる公式




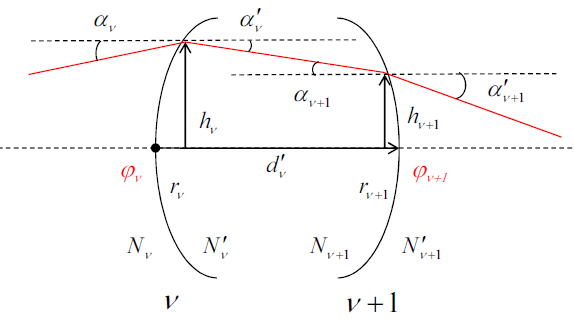
レンズ界面での成立する公式として、以下があげられる

第２、３式は当然の帰結であるが、第４式は光線が媒質中を伝搬するときのどの程度光線の高さが下がるかを表している

第１式は界面での屈折の法則を式にしたものである。（薄肉のときも計算したのでここでは導出は行わない）



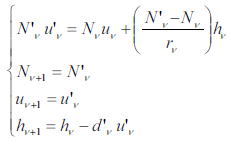
初めて出てきた文字もあるので、それらは以下のように定義している。

さらに上式を界面の屈折と転送によるものとに区別して整理する。



上式を見ると、高さｈと換算傾角αに対して線形性のある式であることに気がつく。

このことは屈折と転送における光線の変化はマトリックスで記述できることを意味する。



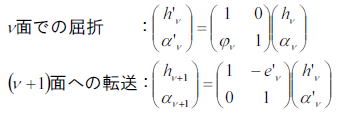
これらのマトリックスが転送と屈折における光線追跡をするためのマトリックスである。

次節のもうすこしこれらの使い方を紹介しようと思う