---

Matrix法（マトリックス法）の使い方


前節で光線追跡用の式とマトリックスまで整理した。光線の成分は傾きと高さ成分からなり、

屈折マトリックスと転送マトリックスの二つで記述することができることを述べた。

この節ではその使い方に関して説明をしていきたいと思う。屈折マトリックスと転送マトリックスは以下のようにかけた。







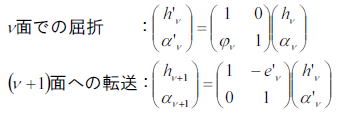
単レンズの場合

何事もまずは単純化したものから取り組むのがよいと思われるので、まずは単レンズに関して光線追跡を行ってみる。

今回の検討はMathematicaで光線追跡の計算を行おうと思う

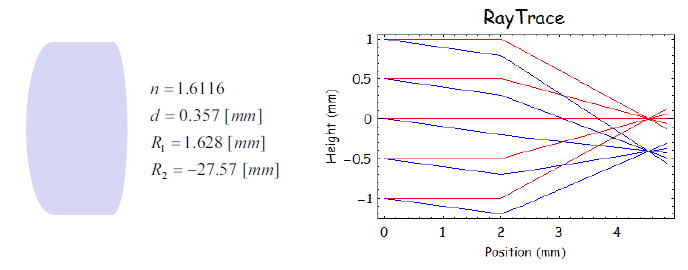
レンズの構成として以下のものを考えよう。

その時の光線追跡をしたものが右の図である。画角を変えたものを色を変えて記載している

物体からレンズまでの距離を２ｃｍ（グラフで言うと２ｃｍの位置にレンズがある））として平行光線を入れている

光線追跡では焦点距離が画角にかかわらずおおよそ２．６ｃｍ程度のところにある。

つまり、主平面の位置が２．６ｃｍのところにある。



厚肉レンズでは焦点距離は以下の式で計算できることを示した。



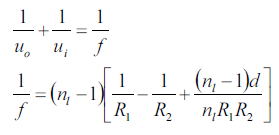
それで焦点距離を計算してみるとｆ＝２．５ｃｍとなる

よって、上記の光線追跡と計算とは一致することがわかる

最後に、ここでの計算は光線高さ（光軸からの高さ）で基本的にはレンズの厚みは変化するはずであるが、
その点に関しては考慮されていない。実際多くの本がそのように記載されており、実際もっと厳密に計算使用するならば、
考慮すべき問題である。


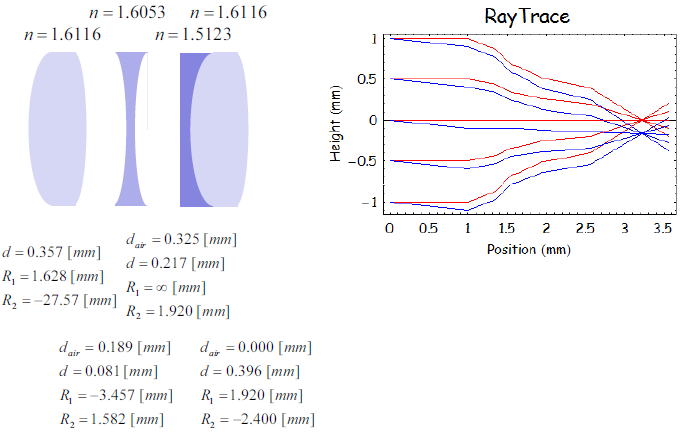
複数レンズ（テッサー・レンズ）の場合


上記ではおなじみの単レンズで計算を行ってみたが、次にレンズが４枚ある時の光線追跡を行ってみようと思う

例としてはテッサー・レンズを利用したわけだが、Hechtの光学Iのほうに結果が書かれており

計算が正しいかチェックできるためである。

左側が計算に用いた各レンズの仕様で、右側がそのレンズ仕様に対して

画角の異なる５つの平行光線に対して光線追跡を行った結果である。

レンズの第一面は１ｃｍのところに置かれたとして計算している。