
収差とは
今まで紹介した第1次理論は近似にすぎないが、正確な光線追跡や試作した光学系の測定を行うと、確かに近軸理論では説明できない。
ガウス光学という理想化した状況とのそのような不一致を収差(aberration)として知られている。
収差には以下の二つに分類することができる。
①色収差(Chromatic aberration)・・・・・屈折率nが周波数あるいは色の関数であることに起因する
②単色収差(monochromatic aberration)・・・・・準単色光でも発生する収差
②に関してはさらに二つのグループに分類できる。
2-1.球面収差(spherical aberration)、コマ(coma)、非点収差(astigmatism)・・・・・像を不鮮明にして劣化させる単色収差
2-2.像面湾曲(Field curvature)、歪曲(distortion)・・・・・像を変形させる収差
球面は一般に近軸領域でしか完全な像をもたらさない。
これからは、有限な大きさの開口のもとで球面を利用すると、どの種類の収差がどの程度発生するのかを見てみることは
収差を理解するうえで有意義な方法のひとつと思われる。これからはそれらに関して触れていこうと思う。
単色収差
近軸での取り扱いでは、 sinΦ=Φで十分表現できるという仮定の下で成り立っている
そこで、少なくとも正弦関数を第3次までの項を計算に取り入れて、近似をよくする理論のことを第3次理論(Third order theory)という。
第1次理論との差はザイデルが1850年代に詳細に研究し、5つのザイデルの5収差と呼ばれる形となって現れる。
ザイデルの5収差とは、球面収差、コマ、非点収差、像面湾曲、歪曲の5つの収差である。
これからは、もっぱら上記の5つの収差に関して議論していくことにする。
球面収差
近軸領域では、球面状の屈折面における共役点は、
で定められる。しかし、光軸から大きく離れたところhでは、共役点の関係は以下のように修正される。
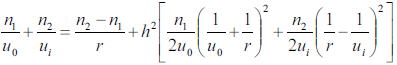
この式が意味することは、物体の高さhがあるとそのhの2乗の効果によって、光線が大きく曲がり
光軸上の集光点が手前に来てしまうことを意味している。
つまり、右辺をすべて焦点距離 f の項と考えるならば物高hによって焦点距離が小さくなる
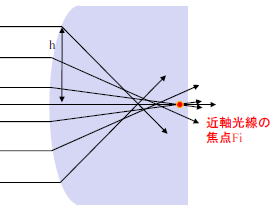
光線が光軸を横切る点と近軸の焦点Fiとの距離はその光線の縦球面収差(longitudinal spherical aberration)として知られている。
上記では球面屈折率分布を持ったレンズに対してどのような球面収差が生じるのかを見た。
では球面ではなかった場合以下の面白い例があるので、その説明をしよう。
開口と焦点距離が固定されているとき、球面収差量は物体の距離とレンズ形状の双方によって変化する。
そのため、例えば平行光(物体位置無限)を入射したとき、レンズの表裏を変えただけで球面収差量が劇的に改善されることがある。
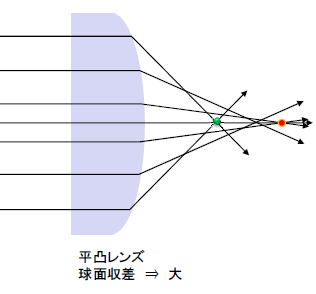
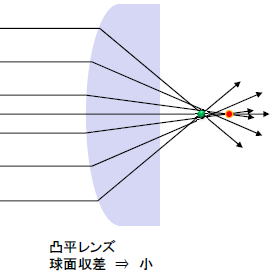
上記の図はそのことを表している。平凸レンズにおいて平行光をレンズの裏面だけで曲げようとする場合、
球面収差が大きく出ていることが分かる。また凸平レンズの場合凸面で緩やかに変化させて、
さらに平面でも変化させて光軸上に集光させる。このような場合、詳細には3次収差論の式をきちんと追っていく必要があるのだが、
球面収差が非常に抑えられた形になる。(3次収差論での球面収差の記述は今後行うこととして、ここでは定性的な話にとどめる。)
