---

単色収差

コマ収差

次にコマ（coma）、またはコマ収差(comatic aberration）に関して説明しよう。

コマ収差の起源は軸外の点の像の劣化をもたらす、主要な単色収差である。

その起源は、主平面を平面として扱えるのは近軸領域のみであり、現実には主平面は曲面であることに由来する。

したがって、球面収差がないとすれば、光軸に平行な光線束は軸上のFiの１点に集光するので、

軸上に像点がある場合は問題がないが、主平面が曲がっているために、横倍率は光線の高さごとに異なることを意味する。

このことは軸外の像点で光線束が斜めの場合が大問題で、光線の高さごとに横倍率が異なることは下の図に示したように、

光線の高さが高い（レンズの外側）ほど主光線（主点を通る光線）から大きく外れることを意味する。

下の図のように主光線より外側に光線が集光する場合を正のコマと呼び、また主光線より内側の場合負のコマと呼ぶ

　　　　　

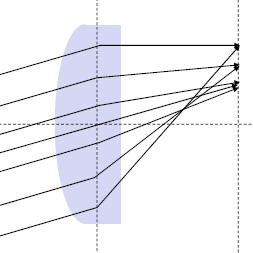
もう少し詳しく幾何学的点像の形成を図で説明するために、下の図を示す。



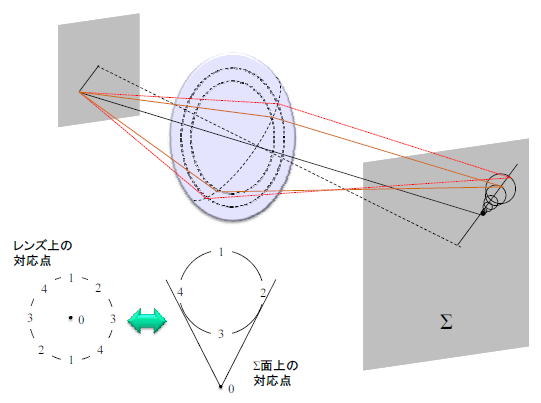
レンズの輪帯上の点１−２−３−４・・・がコマ収差円（comatic circle）と名付けられた円周形状の像を像面Σ上に形成する

収差には正負のコマの呼び方以外像面で０−１の距離のコマ収差を子午的コマ収差（tangential coma）で、

０−３の距離のコマ収差を球欠的コマ収差（sagittal coma）である。

コマ収差は彗星の尾にその名の由来があるように非対称な形状であることを主たる理由に、

すべての収差の中で最悪の収差であるとよく言われる

コマ収差は、球面収差と同様にレンズ形状に依存している。

下図がそのことに関してまとめてある。



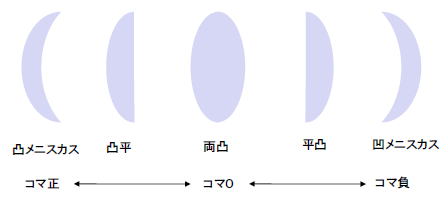
また、次のことを知っていると便利なことが多い。

ある物体距離において、単レンズのコマを正確にゼロにできるという事実がある。

例えば、so＝∞の場合は凸平の形状を持ったレンズはコマ収差を最小にする効果を持つ。

さらに幸いなことにこの事実は、球面収差を最小にする形状と近いことをも覚えておくと実験のとき便利だろう。

参考にまでだが、実際有限の距離に共役点がある場合、既製品（規格品）のレンズで光学系をどのように構成したらよいだろうか？

規格品のレンズでは自分の設定した物体と像の距離に対して、収差をよく抑え込まれたレンズを購入することは難しい。



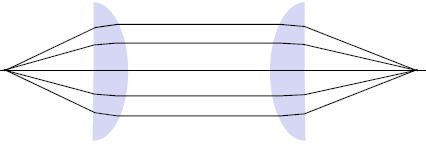
そのため、上図のように無限遠の共役点に対してよく補正されたレンズはいくらでもあるため、

それらを対にして利用することが有効な代替案であることを覚えておくとよいだろう。

正弦定理

光学的正弦定理（Optical Sine theorem）に関して証明は行わないが説明する。

この定理は１８７３年にアッべとヘルムホルツによって独立に発見された定理である。その内容は、



である。ｈは高さ、ｎは屈折率、αは光線の傾き角度であり、開口の大きさは任意である。

コマがゼロであるためにはすべての光線に対して、



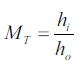
が成立することである。光学的正弦定理を用いてMTに代入して、コマ収差のない必要十分条件は、



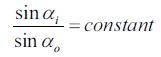
を満たすこと、つまり、正弦条件（sine condition）をみたすことが必要であることを意味する