---

　この節では単色光でステップインデックスファイバの光伝搬を電磁気学を用いて説明する

空間分布

コアでもクラッドにおいても、電場と磁場はヘルムホルツの式を満たしている。

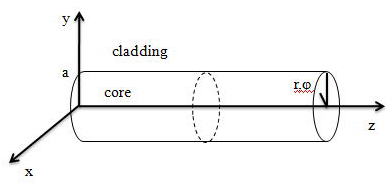
ファイバはシリンドリカル（円柱）座標系に取っておくと対称性の観点からよいので、

この座標系で式を表現することにする。





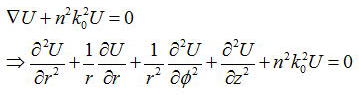
この解のうち興味があるのはｚ方向に伝搬するexp(iβz)である、さらに円周方向にはφのハーモニクスであると仮定すると



であり、これを代入すると、



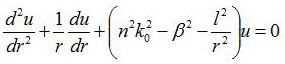
となり、コアとクラッドで以下の定数を定義し、コアとクラッドで解が異なるので、分類して方程式を立てると



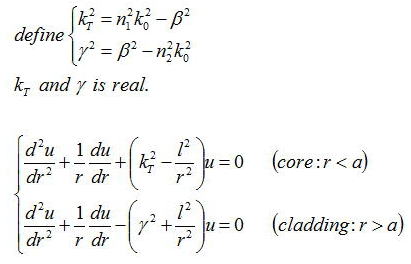
である。この解はベッセル関数を解とする



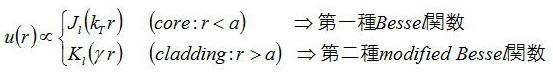
この解の意味するところは、kTが大きくなると振動が大きくなり、γが大きくなると減衰クラッドへの染み出しが小さくなる。

またkTとγの間には以下の関係式がある



と一定の値になる。そのため、コアの直径方向（動径方向）に振動が多い場合は染み出しが大きくなる。

上記の数式をファイバの半径aで規格化した値は重要でVパラメータと呼ばれている。



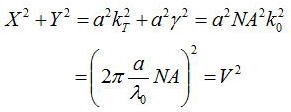
(電場の図を示す予定)