---

　この節ではファイバ内のモードの数がどのようになるのかを計算してみることにする

モード

ほとんどのファイバはクラッドとコアの屈折率の差は小さく、弱いガイドされている。

そのため、前節でみたように、NA^2=n1^2-n2^2なので、NAは小さく近軸（paraxial）である。

よってガイドされた、つまりファイバを伝搬する電磁場はファイバ軸に対して垂直に振動する

電磁場（TEM　transverse electromagnetic）のみと近似することができる。

さらに、二つの直交に偏光した電磁場も区別して、ファイバを伝搬する光にはモードという空間強度分布で分類される。

この直交に偏光した空間強度分布をLinearly Polarized (l,m) modeと呼び、通常 LPlm modeと記述する。

前節でみたように　ｌ　は円周方向のモードを規定し、ｍは動径方向のモードを規定する。

では本題に戻り、ファイバを伝搬するモードの数をどのように決定するのかということを考える

コアとクラッドのr=aでのu(r)関数の連続性を考えると、



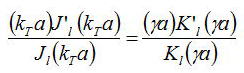
となる。

ここでBessel関数の以下の関係式を満足する



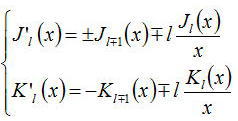
これを用いて上式を整理すると



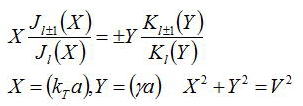
となり、これ式を満たすモード　l　がファイバを伝搬することになる。

上式の右辺と左辺のグラフをそれぞれ描いた。

これら二つの交点が、ファイバ中を伝搬するモードである。左からｌ＝0,1,2・・・で交点の個数がモード伝搬の数である。



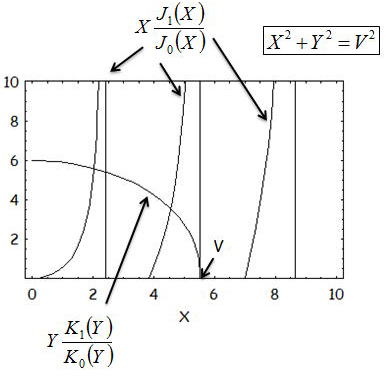
右辺のX軸との交点が結果的にモードの数を決定する。上のグラフはJl（X）＝０の解である。

ファイバ中に１つのモードしか入れないシングルモードファイバの解はグラフには示していないが、

（ｌ−１）の方程式である。このときJ（ｌ−１）（X）＝０の交点がシングルモードを決定する。

その交点はX=２．４０５である。そのためV＝２πaNA/λ＜２．４０５の条件が

シングルモード（SM：single mode）LPlm=LP01が伝搬するNAとコア半径aである。

カットオフ波長λ=730nm、NA=0.13のときのSM伝搬するときのコア直径は

コア径：２a＜4.3um

である。

SMF（Single Mode Fiber）の利点

（１）SM伝搬はもっとも効率のよい閉じ込め効果のある伝搬モードである

（２）MMファイバは複数の伝搬モードがあり、それぞれのモードの群速度が異なるため信号パルスが広がって
となりの信号とまざり０１の信号が分離できなくなる。しかし、SMは伝搬モードがひとつなので信号パルスの重なりはない。

（３）SMはMMよりも強度の減衰率が小さい

（４）MMはモード間のランダム干渉によって、モードノイズ（スペックル）というランダムノイズが発生する