---

　この節ではファイバー転送方法に関してもう少し詳しく調べてみると、

ファイバカプラを用いて光を分岐したり、合波したり、異なる二つの波長を合波したり、分岐したりと

いろいろな方法がありそうであるので、それらに関して方式とその簡単な基本原理をまとめようと思う。

これらのファイバカプラはほとんどが１３００ｎｍや１５５０ｎｍ等の通信波長帯域で開発されている


ファイバカプラの基本原理(モード結合理論)

導波形の光デバイスでは、光導波路に何らかの摂動を加えて、モード間に生じる電力のやり取りを

利用することが多い。ここで、モード結合理論を用いて二つの導波モード間の電力のやり取りを説明する。



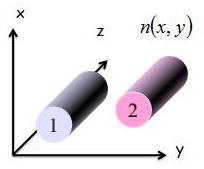
上記のような導波路１と導波路２が結合している（電力のやり取りをしている）と考える

このとき導波路１と２のｚ方向に伝搬する導波モードの電界分布は



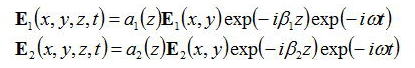
となる。もし二つの導波路が結合していなければ、係数ａは定数となる

ｎとβは導波路の屈折率と導波モードの伝搬定数、ωは光の角周波数である。



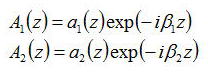
Ａを上記のようにおき、２つのモード間の電力のやり取りを議論する。

ここで以下のモード結合方程式を考える



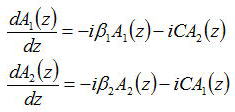
右辺の第一項が導波路を電力のやり取りをしないで伝搬したときの項で、

第二項が電力のやり取りをする項でCが電力のやり取りの大きさを表す。

上式を整理すると、



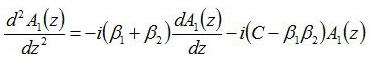
さらに、この方程式の一般解は、



となる。入力端の導波路１と２でそれぞれ振幅A1(０)とA2（０）のモードが入力されたとすると、



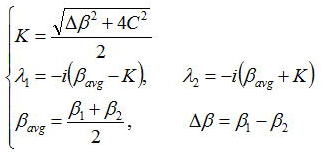
を用いて、以下のようにあらわせる。



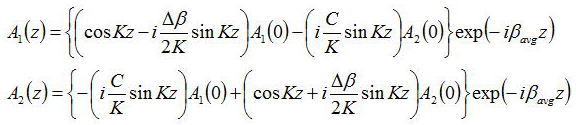
導波路１のみに電力P0が入力され、導波路２に電力が入力されないとすると、





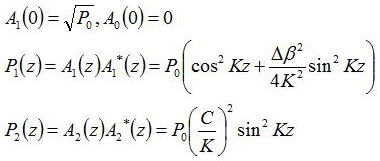
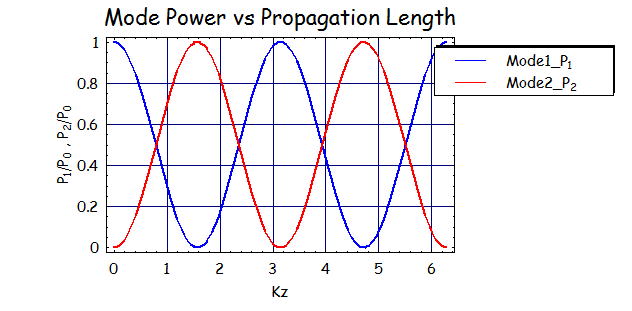
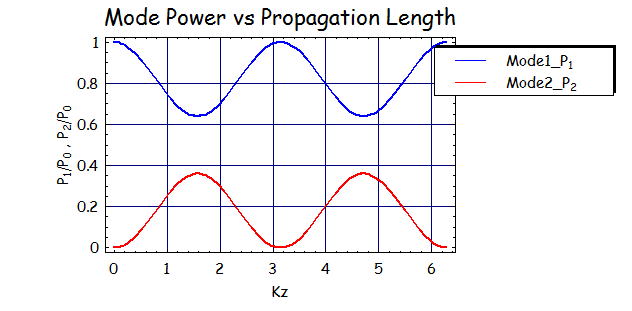
左図は位相整合状態：β１＝β２、C/K=1　

右図は位相不整合状態：β１≠β２

である。

上式からもわかるように、位相不整合状態であるときには最大で電力が移動する量は、P０×（C/K）＾２の量となる。

つまり、両方のモードの伝搬定数が等しく、同期している場合で位相整合がとれる